この記事は、Advent Calendar 2025の18日目の記事になります。
はじめに
こんにちは。サービスイノベーション部の石井です。
業務では大規模モデル*1や需要予測等の技術を活用したマーケティング支援を行なっております。
データサイエンスでは、テキストやグラフといったデータから意味のある特徴表現を抽出する「埋め込みベクトル」を扱う機会が多くあります。OpenAIやGeminiといった主要なプラットフォームでも高性能なエンベディングモデルが提供*2されており、高次元で非常に高い表現能力を持つベクトルを獲得できるようになっています。そして、昨今のモデルでは、同一のモデルから次元の異なる複数の埋め込みベクトルを抽出できる仕組みが実装されています。この技術が「Matryoshka Representation Learning」(以下、MRL)です。
個人的には、この MRL は埋め込みベクトルの短縮という単純な処理だけの話ではなく、より概念に近い特徴表現を抽出することが可能となるのではないかと考えていて、マーケティング関連にも応用が可能な技術だと高く関心を抱いています。 そこで、本記事ではメジャーな大規模言語モデルで共通的に利用されつつ、あまり知られていない MRL について取り扱っていこうと思います。この記事を通して、MRL の理解を少しでも深めて頂ければ幸いです。
本記事で扱う内容
本記事では以下の内容について扱います。
- Matryoshka Representation Learning について
- Matryoshka Representation Learning の実装と性能検証
初めに MRL に関しての簡単な仕組みを説明した後に、いくつかのデータセットに対して MRL を適用した際の次元数と性能の関係を見ていこうと思います。
Matryoshka Representation Learning とは
Matryoshka Representation Learning(MRL)*3 はその名の通り、ロシア人形であるマトリョーシカになぞらえて設計された表現学習のフレームワークです。
埋め込みベクトルにおける表現の質を保ちながら次元を削減する手法として、単一の埋め込みベクトルの中に様々な粒度の情報が入れ子構造で格納されるようにモデルを学習するアプローチにてこれを実現します。この入れ子構造がマトリョーシカに似ていることからこのような命名をされています。

具体的には、埋め込みベクトルの先頭 n 次元を取り出すだけで、任意のサイズの埋め込みベクトルとして利用可能な状態を目指して学習をします。高い表現能力を備えた表現を利用した場合は高次元の埋め込みベクトルを、速度やコストを優先する場合は部分的な低次元の埋め込みベクトルを任意の長さで選択して利用することが可能となります。これにより、単一モデルから複数スケールの表現を得られるため、エッジデバイスやタスクなどの制約事項に合わせた埋め込みベクトルの柔軟な対応を可能にします。
基本概念
続いて、MRLの仕組みについて説明しようと思います。
従来の表現学習手法では Transformer ベースの文脈を考慮した表現学習が中心となっており、学習および推論の両方で複雑で高コストの処理を経て、固定された次元数 D の埋め込みベクトルを学習します。 一方、MRL では固定された次元数 D の埋め込みベクトルを獲得する点は同じですが、この埋め込みベクトルの最初の m 次元だけを取り出した部分埋め込みベクトルについても有効な表現となるように学習を誘導します。

MRL の仕組みは非常に単純で、まず入力データからエンコーダーを用いて最大次元 D の集合を得ます。この最大次元 D の集合に対して、各次元 d の長さを取り出した部分ベクトル z を抽出します。そして、この部分ベクトル z に対して、対照学習で広く使われる InfoNCE Loss*4 などの損失関数により各次元 d 毎の損失を計算し、最後に損失の和を目的関数としてパラメータを学習していきます。
これにより学習より得られた埋め込みベクトルは最大次元 D は当然のことながら、短縮された次元数 d の部分ベクトルにおいても同様の表現能力を有するようになっていきます。ただし、絶対的な次元数が減るに従って表現できる能力には限界が生じるため表現能力が完全に維持できるわけではない点にはご留意ください。
メリット
MRL の最もわかりやすい効果はこれまでにも述べてきたように1つのモデル、1つの埋め込みベクトルから、複数の次元数の埋め込みベクトルを生成できる柔軟性です。この柔軟性により、再学習不要でユースケースに合わせた適切な埋め込みベクトルを選択・利用することが可能となり、実世界で様々な性能と速度のトレードオフを調整した活用ができます。 例えば、情報検索システムにおいては、低次元の埋め込みベクトルを検索インデックスを構築する際に用いて低レイテンシを実現しながら、検索結果上位の検索精度が求められる場面では高次元の埋め込みベクトルを用いてリランキングすることで高性能かつ高速度なシステムが実現できるようになります。
また、先ほどの基本概念の説明より理解頂けているかと思いますが、MRL 自体はモデル非依存な技術となります。表現学習をするためのモデル側アルゴリズムに制約がないため、分析者が利用したいアルゴリズムに対して損失関数の制約を加えることで簡単に MRL の恩恵を受けることができます。そのため、モデル構築時には精度に注力した分析を行い、ベースラインを上回る精度が確認できた後で、MRL を取り入れて実運用を想定した性能面での調整といった精度と性能をしっかり切り分けた開発ができるようになると考えられます。
論文内でも様々なドメインやタスクにおいて MRL の有効性を実証するために、 ResNet や ViT などの画像形式から BERT や ALIGN といったテキスト形式のアルゴリズムに対して MRL を適用した場合の評価実験をしていますので汎用性の高さが理解できるかと思います。より詳細を把握されたい方は本家の論文も参考に見てください。
MRLを試してみる
さて、MRL をサンプル実装で試していきます。
ここまでは理論的な話が中心でしたので、以降では具体的な実装を介して感覚的に理解を深めてもらえればと思います。
テキストデータ
まずは分かりやすいところからテキストデータに対して MRL を適用した例をご紹介しようと思います。
今回は簡単のために既に MRL を適用した学習済みのモデルを利用していこうと思います。ここで利用するモデルは 「sentence-embedding-japanese」というモデルを使っていきます*5。 加えて、検証データには livedoor ニュースコーパス*6のデータセットを用いて評価をしていきます。
各文章に対して、sentence-embedding-japanese モデルにて異なる次元数の埋め込みベクトルを抽出し、得られた埋め込みベクトルを入力として文章カテゴリを当てる文書分類タスクを題材として、次元数と予測精度の関係を見ていこうと思います。また、livedoor ニュースコーパスには9つのカテゴリが含まれているのですが、今回は理解しやすさを優先するために「it-life-hack(ITライフハック)」と「topic-news(トピックニュース)」のカテゴリに絞って二値分類問題として解きます。

こちらが今回のサンプルコードとなります。 まずは livedoor ニュースコーパスのデータセット読み込みとデータ分割のコードです。
import os import glob import numpy as np import pandas as pd from tqdm import tqdm from sklearn.manifold import TSNE from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score, roc_auc_score from sklearn.linear_model import LogisticRegression import seaborn as sns import matplotlib.pyplot as plt from sentence_transformers import SentenceTransformer # ファイルから文章に該当する部分を抽出する処理 def extract_main_txt(file_name): with open(file_name) as text_file: text = text_file.readlines()[3:] text = [sentence.strip() for sentence in text] text = list(filter(lambda line: line != '', text)) text = ''.join(text) text = text.translate(str.maketrans( {'\n': '', '\t': '', '\r': '', '\u3000': ''})) return text # ローカル保存した livedoor ニュースコーパスの読み込み def load_data_livedoor(filepath): categories = [name for name in os.listdir( filepath) if os.path.isdir(filepath + name)] list_text = [] list_label = [] for cat in categories: text_files = glob.glob(os.path.join(filepath, cat, "*.txt")) body = [extract_main_txt(text_file) for text_file in text_files] label = [cat] * len(body) list_text.extend(body) list_label.extend(label) df = pd.DataFrame({'text': list_text, 'label': list_label}) return df # パラメータ設定 label_true = "it-life-hack" # 正解ラベルとして扱うカテゴリ label_false = "topic-news" # 不正解ラベルとして扱うカテゴリ D_max = 1024 # 最大次元数 matryoshka_dims = [32, 64, 128, 256, 512, 1024] # MRLで指定する次元数 model_name = "hotchpotch/static-embedding-japanese" # 言語モデル名 # livedoorデータの読み込み df_text = load_data_livedoor("datasets/livedoor/text/") df_text = df_text[(df_text.label == label_true) | (df_text.label == label_false)] df_text['label'] = df_text['label'].map({label_false: 0, label_true: 1}) # 学習・テスト用のデータ分割 df_text_train = df_text.groupby('label').sample(frac=0.8, random_state=42) df_text_test = df_text.drop(df_text_train.index)
次いで MRL を適用した sentence-embedding-japanese モデルによる埋め込みベクトル抽出と各次元での埋め込みベクトルによる文書分類タスクの評価を行うコードを以下に記載します。
# 表現ベクトルに基づくモデル評価 def cal_classfication(train_repr, train_label, test_repr, test_label): # ロジスティック回帰による学習・推論 lr = LogisticRegression() lr.fit(train_repr, train_label) y_pred = lr.predict(test_repr) # 各評価指標の計算 cmat = confusion_matrix(y_true=test_label, y_pred=y_pred) accuracy = accuracy_score(y_true=test_label, y_pred=y_pred) precision = precision_score(y_true=test_label, y_pred=y_pred) recall = recall_score(y_true=test_label, y_pred=y_pred) f1 = f1_score(y_true=test_label, y_pred=y_pred) auc = roc_auc_score(test_label, y_pred) return cmat, accuracy, precision, recall, f1, auc # 混合分布のヒートマップ可視化 def visualization_heatmap(matrix): fig, ax = plt.subplots(figsize=(8,6)) sns.heatmap(matrix, cmap='Blues', annot=True, fmt="d", cbar=False) plt.ylabel('Actual') plt.xlabel('Predicted') plt.show() # T-SNEによるベクトル可視化 def visualization_tsne(result_repr, result_labels): unique_labels = np.unique(result_labels) colors = ['#b3d5f5', '#12477d'] # T-SNEによる次元削減 tsne = TSNE( n_components=2, # 圧縮後の次元数 perplexity=30, # データ点の近傍数 max_iter=1000, # 最適化のイテレーション回数 random_state=42 # 再現性のための乱数シード ) tsne_results_mrl = tsne.fit_transform(result_repr) # 埋め込みベクトルを2次元圧縮した際のプロット plt.figure(figsize=(10, 8)) for i, label in enumerate(unique_labels): indices = np.where(result_labels == label)[0] plt.scatter( tsne_results_mrl[indices, 0], tsne_results_mrl[indices, 1], c=colors[i], label=f'Label {int(label)}' ) plt.title('T-SNE visualization (livedoor datasets)') plt.xlabel('T-SNE Component 1') plt.ylabel('T-SNE Component 2') plt.ylim(-25, 25) plt.xlim(-25, 25) plt.legend() plt.grid(True) plt.show() # 埋め込みベクトルを用いた次元数毎の性能計算 results = {} for dim in tqdm(matryoshka_dims): _df_text_train = df_text_train.copy() _df_text_test = df_text_test.copy() train_data, train_label = _df_text_train['text'], _df_text_train['label'] test_data, test_label = _df_text_test['text'], _df_text_test['label'] # モデルロード model = SentenceTransformer(model_name, device="cuda", truncate_dim=dim) # 表現抽出 train_repr = model.encode(train_data.to_numpy()) test_repr = model.encode(test_data.to_numpy()) # 入力表現を用いたクラス分類評価 cmat, acc, precision, recall, f1, auc = cal_classfication( train_repr, train_label, test_repr, test_label ) # 混合分布の可視化 visualization_heatmap(cmat) # t-SNEによる表現可視化 visualization_tsne(test_repr, test_label) # 結果格納 result.update( accuracy=acc, precision=precision, recall=recall, f1=f1, auc=auc ) results[dim] = result
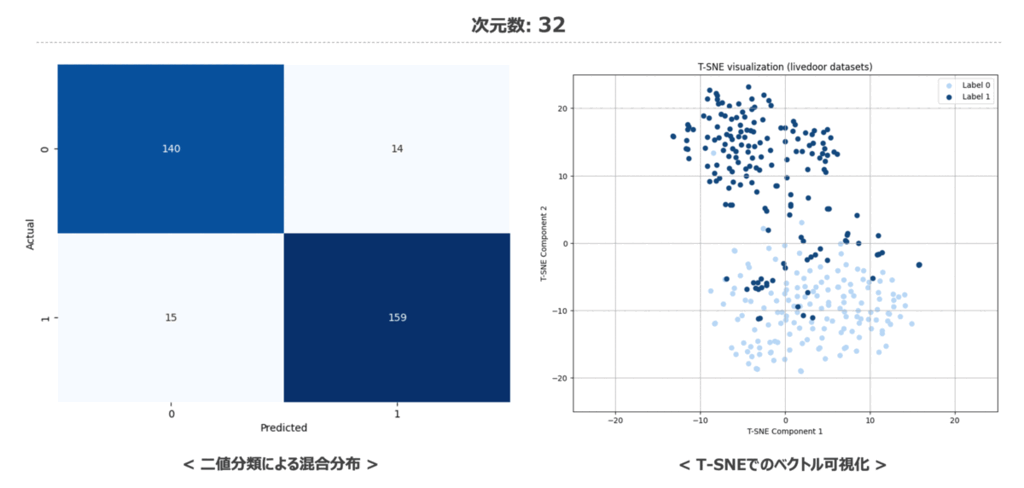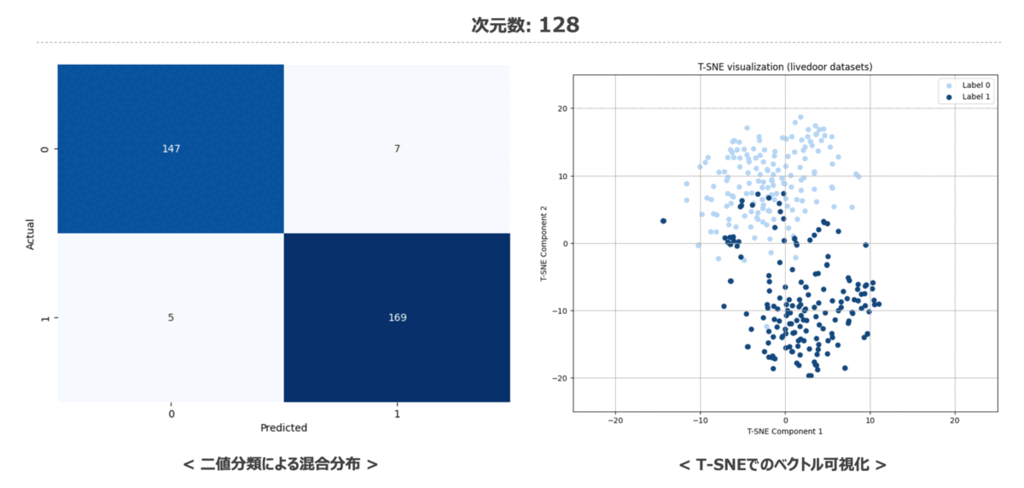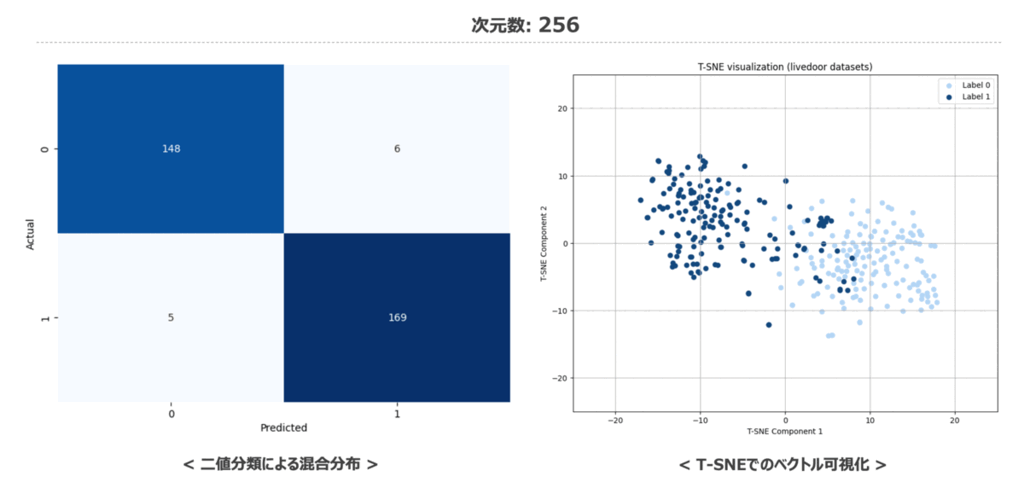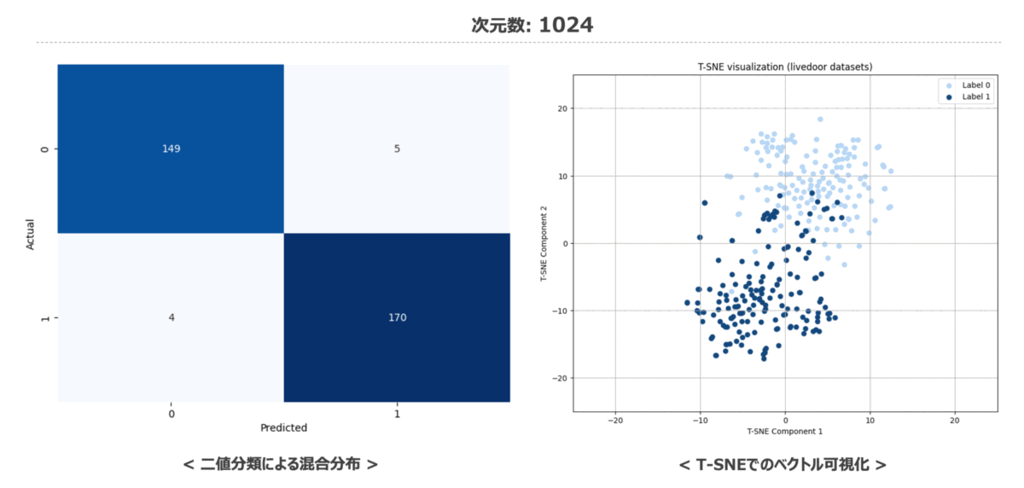
コードを実行した結果は以下の通りとなりました。 次元数が32次元の場合は少し精度が落ちますが、128次元あれば以降の高次元ベクトルと比較しても見劣りしないくらいの精度であることがわかります。

加えて、次元数を変化させた際の二値分類結果の混同行列と特徴量空間の変化を載せておきます。 特徴量空間の可視化内容を見てみても低次元から高次元に遷移する中で大きく分布が変わっていないことか分かるかと思います。
時系列データ
次いで、時系列データに対しても同様の効果が得られるのかを確認してみます。
時系列データから表現抽出を行う仕組みとして TS2Vec*7 を採用して、当該技術に MRL を適用して試していこうと思います。
TS2Vec は時系列データに対して自己教師あり学習を用いた表現学習を行うためのフレームワークとなります。 技術的特徴を簡単に述べておきますと、Hierarchical Contrastive Learning という機構を導入して時系列全体のパターンと局所的な変動を捉えることを可能にして、時系列データが持つ複雑なパターンからロバスト性の高いデータ表現を獲得することを実現する技術となります。本記事の中では TV2Vec についての詳細な説明は省略しますが、興味を持たれた方は是非本家の論文を参照してみてください。
記事内で用いるデータには 「UCR Time Series Classification Archive」で公開されている ECG200*8 のオープンデータを用いていきます。テキストデータの時と同様に獲得した埋め込みベクトルを用いて時系列データを分類するタスクにて次元数と予測性能の関係を評価していきましょう。
まずは TS2Vec を MRL に適用させるために、次元数毎の対照損失を積算するマトリョーシカ損失関数の定義と学習ループ内でマトリョーシカ損失関数を用いて誤差伝播させるための実装を行います。特に今回は実装箇所を最小限にするために、既存の TS2Vec クラスを継承した TS2Vec_MRL クラスを新たに定義して、変更が必要な部分のみをオーバーライドする形で対応していきます。マトリョーシカ損失関数(matryoshka_contrastive_loss)とマトリョーシカ損失関数に変更した学習ループの実装(TS2Vec_MRL)は以下に示します。
マトリョーシカ損失関数のソースコード
import torch from torch import nn import torch.nn.functional as F def matryoshka_contrastive_loss(z1, z2, M, alpha, temporal_unit=0): total_loss = 0.0 for d_i in M: loss = torch.tensor(0., device=z1.device) d = 0 z1_trunc = z1[..., :d_i] z2_trunc = z2[..., :d_i] while z1_trunc.size(1) > 1: if alpha.get(d_i, 1.0) != 0: loss += alpha.get(d_i, 1.0) * instance_contrastive_loss(z1_trunc, z2_trunc) if d >= temporal_unit: if 1 - alpha.get(d_i, 1.0) != 0: loss += (1 - alpha.get(d_i, 1.0)) * temporal_contrastive_loss(z1_trunc, z2_trunc) d += 1 z1_trunc = F.max_pool1d(z1_trunc.transpose(1, 2), kernel_size=2).transpose(1, 2) z2_trunc = F.max_pool1d(z2_trunc.transpose(1, 2), kernel_size=2).transpose(1, 2) if z1_trunc.size(1) == 1: if alpha.get(d_i, 1.0) != 0: loss += alpha.get(d_i, 1.0) * instance_contrastive_loss(z1_trunc, z2_trunc) d += 1 total_loss += loss return total_loss
TS2Vec_MRL クラスのソースコード
import numpy as np import torch import torch.nn as nn from torch.utils.data import TensorDataset, DataLoader from .ts2vec import TS2Vec from .losses import matryoshka_contrastive_loss from utils import take_per_row, split_with_nan, centerize_vary_length_series, torch_pad_nan class TS2Vec_MRL(TS2Vec): # コンストラクタ def __init__( self, input_dims, output_dims=320, hidden_dims=64, depth=10, device='cuda', temporal_unit=0, mrl_dims: list = None, mrl_dims_weight = None ): super().__init__( input_dims=input_dims, output_dims=output_dims, hidden_dims=hidden_dims, depth=depth, device=device, temporal_unit=temporal_unit ) # MRL設定の検証と保存 if mrl_dims is None or not mrl_dims: raise ValueError("TS2Vec_MRL requires 'mrl_dims' (e.g., [32, 64, 320]).") self.mrl_dims = sorted(list(set(mrl_dims))) # MRL学習時の重みづけのバリデーション if mrl_dims_weight is None or not mrl_dims_weight: raise ValueError("TS2Vec_MRL requires 'mrl_dims_weight' (e.g., [0,5, 0,5, 0,5]).") self.mrl_dims_weight = dict(zip(mrl_dims, mrl_dims_weight)) # 最大次元(output_dims)が mrl_dims に含まれているか確認 if output_dims not in self.mrl_dims: print(f"Warning: Max output_dims ({output_dims}) was not in mrl_dims. It has been added.") self.mrl_dims.append(output_dims) self.mrl_dims = sorted(list(set(self.mrl_dims))) # 最大次元がリストの最後であることを確認 if output_dims != self.mrl_dims[-1]: raise ValueError(f"output_dims ({output_dims}) must be the largest value in mrl_dims ({self.mrl_dims})") print(f"[TS2Vec_MRL Enabled] Training with dimensions: {self.mrl_dims}") print(f"Parent class (TS2Vec) initialized with max_dim={output_dims}") # マトリョーシカ損失関数を利用した学習ループの定義 def fit(self, train_data, n_epochs=None, n_iters=None, verbose=False): assert train_data.ndim == 3 if n_iters is None and n_epochs is None: n_iters = 200 if train_data.size <= 100000 else 600 # default param for n_iters if self.max_train_length is not None: sections = train_data.shape[1] // self.max_train_length if sections >= 2: train_data = np.concatenate(split_with_nan(train_data, sections, axis=1), axis=0) temporal_missing = np.isnan(train_data).all(axis=-1).any(axis=0) if temporal_missing[0] or temporal_missing[-1]: train_data = centerize_vary_length_series(train_data) train_data = train_data[~np.isnan(train_data).all(axis=2).all(axis=1)] train_dataset = TensorDataset(torch.from_numpy(train_data).to(torch.float)) train_loader = DataLoader(train_dataset, batch_size=min(self.batch_size, len(train_dataset)), shuffle=True, drop_last=True) optimizer = torch.optim.AdamW(self._net.parameters(), lr=self.lr) loss_log = [] while True: if n_epochs is not None and self.n_epochs >= n_epochs: break cum_loss = 0 n_epoch_iters = 0 interrupted = False for batch in train_loader: if n_iters is not None and self.n_iters >= n_iters: interrupted = True break x = batch[0] if self.max_train_length is not None and x.size(1) > self.max_train_length: window_offset = np.random.randint(x.size(1) - self.max_train_length + 1) x = x[:, window_offset : window_offset + self.max_train_length] x = x.to(self.device) ts_l = x.size(1) crop_l = np.random.randint(low=2 ** (self.temporal_unit + 1), high=ts_l+1) crop_left = np.random.randint(ts_l - crop_l + 1) crop_right = crop_left + crop_l crop_eleft = np.random.randint(crop_left + 1) crop_eright = np.random.randint(low=crop_right, high=ts_l + 1) crop_offset = np.random.randint(low=-crop_eleft, high=ts_l - crop_eright + 1, size=x.size(0)) optimizer.zero_grad() out1 = self._net(take_per_row(x, crop_offset + crop_eleft, crop_right - crop_eleft)) out1 = out1[:, -crop_l:] out2 = self._net(take_per_row(x, crop_offset + crop_left, crop_eright - crop_left)) out2 = out2[:, :crop_l] loss = matryoshka_contrastive_loss( # 既存のhierarchical_contrastive_lossを置き換え out1, out2, self.mrl_dims, self.mrl_dims_weight, temporal_unit=self.temporal_unit ) loss.backward() optimizer.step() self.net.update_parameters(self._net) cum_loss += loss.item() n_epoch_iters += 1 self.n_iters += 1 if self.after_iter_callback is not None: self.after_iter_callback(self, loss.item()) if interrupted: break cum_loss /= n_epoch_iters loss_log.append(cum_loss) if verbose: print(f"Epoch #{self.n_epochs}: loss={cum_loss}") self.n_epochs += 1 if self.after_epoch_callback is not None: self.after_epoch_callback(self, cum_loss) return loss_log
上記の実装が完了したら定義したクラスを利用して MRL を学習・評価するコードを記述します。
from tqdm import tqdm import torch import numpy as np import pandas as pd import dateutil import sklearn from sklearn.manifold import TSNE from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score from sklearn.linear_model import LogisticRegression from sklearn.metrics import roc_auc_score from sktime.datasets import load_arrow_head, load_italy_power_demand import seaborn as sns import matplotlib.pyplot as plt from ts2vec import datautils from ts2vec.utils import * from ts2vec.models import TS2Vec_MRL # パラメータ指定 batch_size=16 hidden_dims=64 depth=10 lr=0.001 output_dims=1024 matryoshka_dims = [32, 64, 128, 256, 512, 1024] matryoshka_dims_weight = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0] matryoshka_dims_max = matryoshka_dims[-1] device='cuda' # データ読み込み(EGC200) train_data, train_label, test_data, test_label = datautils.load_UCR('ECG200') # TS2Vec_MRLのインスタンス生成 model_mrl = TS2Vec_MRL( input_dims=train_data.shape[-1], output_dims=matryoshka_dims_max, mrl_dims=matryoshka_dims, mrl_dims_weight=matryoshka_dims_weight, hidden_dims=hidden_dims, depth=depth, device=device, ) # モデル学習 model_mrl.fit( train_data, n_epochs=50, verbose=True ) # 学習したモデルより埋め込みベクトル抽出 train_repr_mrl = model_mrl.encode(train_data, encoding_window='full_series') test_repr_mrl = model_mrl.encode(test_data, encoding_window='full_series') # 埋め込みベクトルを用いた次元数毎の性能計算 results = {} for dim in tqdm(matryoshka_dims): result = {} # 指定した次元数に応じた表現抽出 train_repr = train_repr_mrl[..., :dim] test_repr = test_repr_mrl[..., :dim] # 入力表現を用いたクラス分類評価 cmat, acc, precision, recall, f1, auc = cal_classfication( train_repr, train_label, test_repr, test_label ) # 混合分布の可視化 visualization_heatmap(cmat) # t-SNEによる表現可視化 visualization_tsne(test_repr, test_label) # 結果格納 result.update(accuracy=acc, precision=precision, recall=recall, f1=f1, auc=auc) results[dim] = result
上記コードを実行すると MRL を適用した TV2Vec を介して、時系列データから任意の次元数を選択可能な埋め込みベクトルが獲得できるようになるかと思います。今回得られた埋め込みベクトルを用いて異なる次元数で性能評価を行った結果は以下の通りです。
先ほどのテキストデータの時と同様に埋め込みベクトルの次元数を小さくしても大きな精度劣化が見られないことが分かるかと思います。また、比較対象として MRL を適用しない場合の TS2Vec を水色の線で描画してみると、MRL を適用することで次元数が128次元以下の場合でも精度維持できていることがより鮮明に理解できるかと思います。

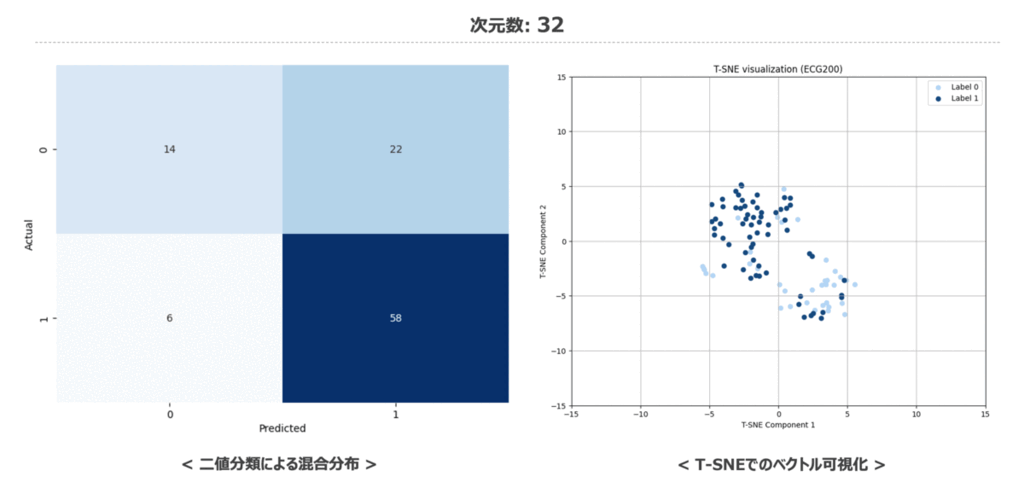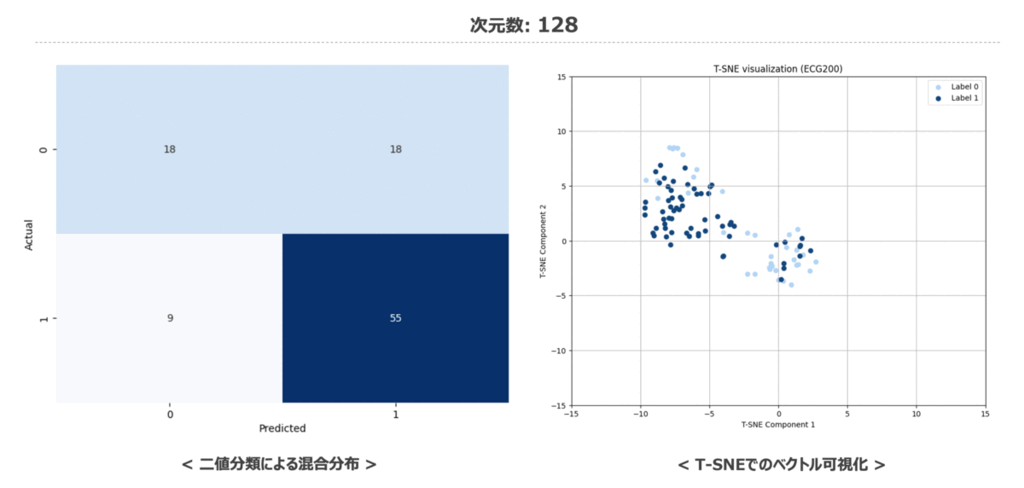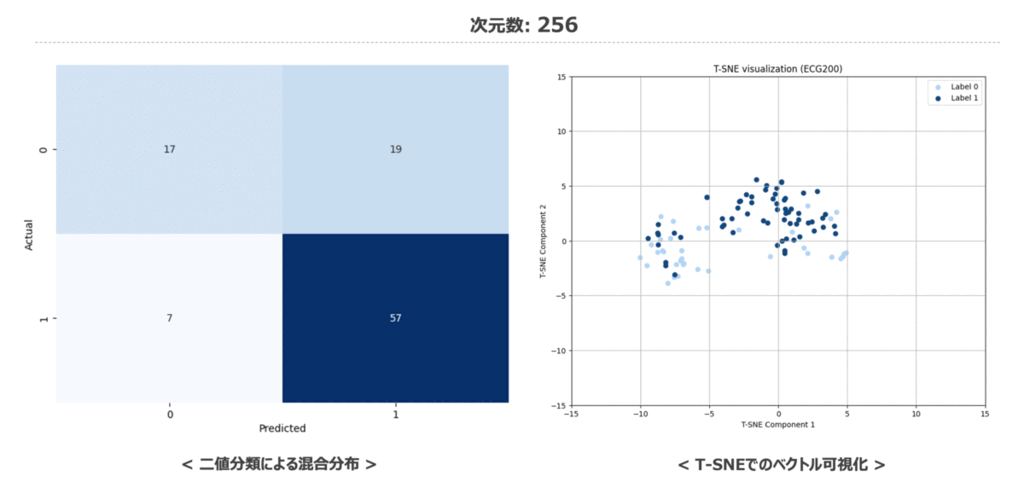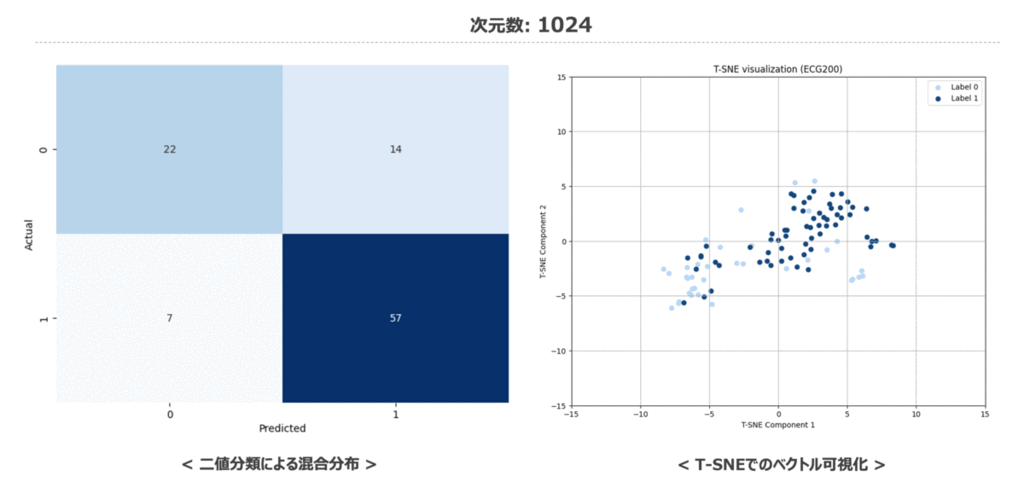
最後に時系列データに対しても次元数を変化させた際の二値分類結果の混同行列と特徴量空間の変化を記載しておきます。 32次元の時から分類タスクにて予測がしっかり当てられているため、1024次元の場合と比較してもマトリクスの色が大きく変化していないですね。低次元でもしっかり意味のある埋め込みベクトルとなっているのは見ていて少し驚かされます。
おわりに
本記事では表現学習の関連技術である Matryoshka Representation Learning をご紹介させていただきました。 最新のエンべディングモデルでは表現能力の高さを獲得するために高次元の埋め込みベクトルとなる場合が多くある一方で、次元数の大きさに比例して計算コストやストレージコストも大きくなることから、同一モデルでユースケースに応じた適切な次元数の埋め込みベクトルを選択できるようになる点は実運用観点で非常に有益な技術だと感じました。 本記事の中ではテキスト、時系列という異なるデータ形式に対して、MRL を適用した場合の次元数と性能の関係を確認してみました。利用するモデルやデータ形式、パラメータ設定によって次元数と性能のトレードオフの関係に違いはありますが、この記事を読んで少しでも皆様が面白い技術だと感じてもられえれば幸いです。
それでは、明日の記事もお楽しみください!
*1:大量かつ多様なデータで訓練され、様々な下流タスクに適用できるよう設計された大規模なAIモデル
*2:OpenAIでは「text-embedding-3-large」で3072次元の埋め込みベクトル、Geminiでは「gemini-embedding-001」で3072次元の埋め込みベクトルを抽出可能
*3:NeurIPS 2022にて発表された「Matryoshka Representation Learning」で提案された表現学習手法
*4:通常の対照学習の損失関数としてよく用いられる。InfoNCE Loss を例として挙げましたが、その他のLoss関数でも対応可能です
*5:Transformerベースではない文書埋め込みモデルになります。static-embedding-japaneseモデルの学習コードについても公開されています
*6:livedoorが公開したニュース記事のテキストデータが含まれるデータセットです。NLP関連の研究開発において広く使用されており、こちらからダウンロードできます。
*7:TS2Vec: Towards Universal Representation of Time Series内で提唱された時系列の表現学習のためのフレームワーク
*8:時系列分類のベンチマークとして広く利用されているデータセットの1つで、心電図波形を示した短変量系列データとクラスラベルが付与されたデータになります。
