NTTドコモR&Dの技術ブログです。

トップ > アドベントカレンダー2024 > Pyomo×SCIPは組合せ最適化にて最強… 覚えておけ

Pyomo×SCIPは組合せ最適化にて最強… 覚えておけ

アドベントカレンダー2024 数理最適化 python

はじめに

NTTドコモ クロステック開発部の佐藤です。普段は農業で画像認識技術を活用することに取り組んでまして、病気の葉っぱの検出に勤しんでおります。 こちらの記事では、組合せ最適化問題を解く上で、現状ベストプラクティスのひとつではと思う実装方法についてご紹介したいと思います。 対象読者は、初めて数理最適化の実装をしてみるという方や、何度かはやったことあるけどより良い方法を知りたいという方向けです。 タイトルの通り主観も入り気味ですが、ご容赦下さい！

組合せ最適化問題とは

組合せ最適化問題とは、何らかの制約条件のもと、同じく何らかの目的関数を最大化ないし最小化させるような、決定変数の組合せを求める問題です。 実は世の中このような問題であふれていて、例えば以下のようなものがあります。

  • (A) リスクを抑えた投資商品のポートフォリオを決める問題
  • (B) ナップサックに入る範囲で、遠足に持っていくお菓子の種類と個数を決める問題
  • (C) 忘年会で普段話さない人同士が近くに座るような座席配置を決める問題

決定変数の種類

このような組合せ最適化問題は、目的関数と制約条件の形で定式化できる訳なのですが、決定変数と式の構造によって種類が分かれます。決定変数は以下の3種類です。

  • 実数（連続な数）のみ
  • 整数のみ
  • 実数と整数が混在

例えば、上述の(A)で投資銘柄の構成割合を決める場合は、決定変数が実数となりますが、(B)の場合は決定変数が整数になり、そのような問題を整数計画問題と呼びます。 更に決定変数が整数だけでなく実数も混在する場合は、混合整数計画問題と呼称します。

決定変数が連続な場合は、勾配計算を活用して効率的に良解を探索するアルゴリズムなどがあり、比較的速く計算を終えることができます。 一方で決定変数に整数を含む場合には、解空間が離散的であるため勾配計算が活用できず、一般に計算コストが高くなる傾向にあります。 求解が難しく実装手段の吟味が必要であろう観点から、以降この記事では整数計画問題および混合整数計画問題に着目してお話していきます。

式の構造の種類

組合せ最適化問題は、式の構造によっても以下に大別されます。

  • 線形　：目的関数と制約条件ともに決定変数の一次式で表現できるもの
  • 非線形：目的関数か制約条件のどちらかに、決定変数同士の積など非線形の項が存在するもの

整数計画問題や混合整数計画問題であっても式が線形であれば、無償で利用できるライブラリも多くあり、実装手段で困ることはあまりなさそうです。 しかし非線形の場合、実装手段がやや限られてくるため、以降で紹介していきたいと思います。 なお非線形の中でも、二次の問題について扱います。

定式化の例

非線形な整数計画問題の例として、上述の(C)の忘年会の配席問題を挙げます。具体的には下式の通り、普段関わりを持たない人同士が同テーブルに着くように、 N人の出席者を M台のテーブルに割り当てるというオリジナル問題です。

\displaystyle \begin{aligned} & \underset{x} {\text{minimize}} && \sum^{M}_{k=1}\sum^{N}_{j=1}\sum^{j-1}_{i=1}D_{ij}\cdot x_{ik}\cdot x_{jk} \\ & \text{s.t.} &&\sum _{k}x_{ik}=1 \quad \forall i \in \{1, \dots, N\}, \\ & && {} \sum _{i}x_{ik}\leq S \quad \forall k \in \{1, \dots, M\}, \\ & && x_{ik}\in \{0,1\}. \\ \end{aligned}

式の意味は以下です。

  • 決定変数：ユーザ iがテーブル kに座るか否かを示す2値変数 x_{jk}
  • 目的関数：同じテーブルに座る出席者同士の関係度合い d_{ij}の総和を最小化
  • 制約条件：
    • 各ユーザーは1つのテーブルにのみ座る
    • 各テーブルの最大着席人数は S人まで

ユーザー同士の関係度合い d_{ij}は便宜上定めた係数行列です。設定方法としては、職場であれば同じチームに属している場合や入社年次が近い場合に、普段から関わりが多いと見なして高い値とする等が考えられます。

実装のアプローチ

求解手段としては大きく厳密解法と近似解法があり、以下でそれぞれについて述べていきます。

近似解法で解く

近似解法は、計算の仕組みとして最適解かは保証していないが、実行可能な良解を出力するアルゴリズムです*1。例えば遺伝的アルゴリズム（GA）等が挙げられますが、近傍解の探索と暫定解の更新を繰り返すような計算手続きが行われます。ライブラリとしては、pymooがGAや粒子群最適化（PSO）など複数のアルゴリズムに対応しており、多目的最適化に拡張も可能なため良さそうです。ただ良解を得るには、近傍探索や解更新の処理を問題に合わせてカスタマイズしなければならないケースもあり、試行錯誤の工程を覚悟しておく必要があります。また良解が得られたとしても、厳密解法で得られる解には及ばないため、まずは厳密解法を優先して検討すべきと考えています。

厳密解法で解く

厳密解法は、計算の仕組みとして最適性が保証された解を出力するアルゴリズムで、分枝カット法等が挙げられます。計算手順としては樹形図のように組合せの場合分けを進めて解を列挙していきますが、既に見つかった暫定解より良解が見込めない枝については、それ以上の場合分けを進めず剪定するといった効率化の対処が取られています。組合せを列挙していく性質上、計算時間は決定変数の数に依存して長くなる傾向にありますが、式に拠っては短く済む場合もあるため、実装して確認してみることを勧める次第です。このような厳密解法の実装アプローチは、以下の2つに大別されます。

線形の式に帰着させて解く

補助変数を導入する等して、線形な式に同値変形してから解くアプローチです。 前述の忘年会の配席問題だと、 決定変数同士の積 x_{ik}\cdot x_{jk}を意味する補助変数 y_{ijk}を導入して、以下のように変形できます。

\displaystyle \begin{aligned} \underset{x,y} {\text{minimize}} \quad & \sum_{k=1}^M \sum_{j=1}^N \sum_{i=1}^{j-1} D_{ij} \cdot y_{ijk} \\ \text{s.t.} \quad & \sum_{k=1}^M x_{ik} = 1 \quad \forall i \in \{1, \dots, N\}, \\ & \sum_{i=1}^N x_{ik} \leq S \quad \forall k \in \{1, \dots, M\}, \\ & y_{ijk} \leq x_{ik}, \quad y_{ijk} \leq x_{jk}, \quad y_{ijk} \geq x_{ik} + x_{jk} - 1 \quad \forall i < j, \forall k, \\ & x_{ik} \in \{0, 1\}, \quad y_{ijk} \in \{0, 1\}. \end{aligned}

線形に変形することで求解計算の効率化が期待できる反面、補助変数と制約式の数が増えるため必ずしも計算時間が速くなる訳ではないのと、式変形を考える工程が発生するのが難点です。

非線形の式のまま解く

そこで、非線形の式のまま解いてみるアプローチが第一手となり得ます。 非線形の式のまま求解計算するには、混合整数非線形計画問題（MINLP - Mixed Integer Nonlinear Programming）に対応したモデラ―*2 とソルバー*3 を使う必要があります。

以下に主なソルバーの一覧を掲載します。 ご覧の通りMINLPに対応していて無償なものとしてSCIPがあります。

ソルバーの一覧
ソルバー MILP*4 MINLP*5 有/無償 ライセンス
Cbc ✓ 無償 EPL-2.0
SCIP ✓ ✓ 無償 Apache-2.0
GLPK ✓ 無償 GPLv3
Gurobi ✓ ✓ 有償（学術無料） Gurobi License
CPLEX ✓ ✓ 有償（学術無料） IBM License

次に、モデラ―の一覧も同様に掲載します。 モデラ―もMINLPを扱えるものとそうでないものがあり、MINLPを扱えてSCIPにも対応しているのはPyomoとPySCIPOptです。 このうちPySCIPOptは、SCIP専用のモデラ―となってます。 なので、複数のソルバーで計算時間を確認したかったり、高性能なGurobiに差し替える可能性がある場合は、Pyomoを使っておくのが無難と考えます。

モデラ―の一覧
モデラー MILP MINLP 対応可能ソルバー GitHub Stars*6 ライセンス
PuLP ✓ CBC, GLPK, SCIP, Gurobi, CPLEX等 ⭐️ 2.1k MIT
Python-MIP ✓ CBC, Gurobi ⭐️ 542 EPL-2.0
OR-Tools ✓ CBC, GLPK, SCIP, Gurobi, CPLEX等 ⭐️ 11.3k Apache-2.0
Pyomo ✓ ✓ CBC, SCIP, GLPK, Gurobi, CPLEX等 ⭐️ 2.1k BSD
PySCIPOpt ✓ ✓ SCIP ⭐️ 830 MIT
CVXPY ✓ ✓ CBC,GLPK,Gurobi,CPLEX等 ⭐️ 5.5k Apache-2.0
SciPy ✓ 内部ソルバー ⭐️ 13.2k BSD-3-Clause

以上のように、二次までの非線形な整数計画問題や混合整数計画問題を扱う場合は、モデラ―PyomoとソルバーSCIPを使い、まずは非線形の定式のまま厳密解法を実装するのが良いというのが主張になります。

実装の例

モデラ―にPyomo、ソルバーにSCIPを使った実装の例を示します。題材は上述の忘年会の配席問題です。 まず、出席者数 N、テーブル数 M、および1卓の着席可能人数 Sを以下の通り設定します。 出席者同士の関係度合い D_{ij}はダミーの値を作っています。

N = 20
M = 5
S = 4

import numpy as np
def gen_symmetric_matrix(N, D_low, D_upper):
    """対称行列の作成"""
    np.random.seed(111)
    a = np.random.randint(D_low, D_upper, (N, N)) * np.random.binomial(1, 0.2, size=(N, N))
    matrix = np.tril(a) + np.tril(a).T - np.diag(a.diagonal()) * 2
    return matrix

# 関係度合いの行列を作成
D = gen_symmetric_matrix(N, 1, 5)

次に定式化です。Pyomoの記法に乗っ取って、決定変数と目的関数および制約条件を記述していきます。

import pyomo.environ as pyo

def set_decision_variable(model):
    """決定変数の設定"""
    model.user = pyo.RangeSet(0, N - 1)
    model.table = pyo.RangeSet(0, M - 1)
    model.X = pyo.Var(model.user, model.table, domain=pyo.Binary)
    return model

def Obj(model):
    """目的関数の定義"""
    return sum(D[i, j] * model.X[i, k] * model.X[j, k]
               for k in model.table
               for j in model.user
               for i in range(j))

def tables_per_user(model, i):
    """1人につき1テーブルを割り当てる制約"""
    return sum(model.X[i, k] for k in model.table) == 1

def users_per_table(model, k):
    """1テーブルあたりの着席人数の制約"""
    return sum(model.X[i, k] for i in model.user) <= S

def problem_formulate():
    """定式化"""
    model = pyo.ConcreteModel()
    model = set_decision_variable(model)
    model.obj = pyo.Objective(rule=Obj, sense=pyo.minimize)
    model.const1 = pyo.Constraint(model.user, rule=tables_per_user)
    model.const2 = pyo.Constraint(model.table, rule=users_per_table)
    return model

model = problem_formulate()

最後に、最適化計算を実行して結果を取り出します。

# 最適化計算の実行
opt = pyo.SolverFactory('scip')
res = opt.solve(model, tee=True)

# 最適値の表示
print('Optimum Value: ', pyo.value(model.obj))
print(f"Solver Status: {res.solver.termination_condition}")

import pandas as pd
import itertools
def get_rslt_df(model):
    """最適化結果の取り出し"""
    idx_data = list(itertools.product(range(N), range(M)))
    df = pd.DataFrame(idx_data, columns=['user','table'])
    df['X'] = [pyo.value(model.X[i, k]) for i, k in list(idx_data)]
    return df.pivot_table(index='user', columns='table', values='X')

df = get_rslt_df(model)

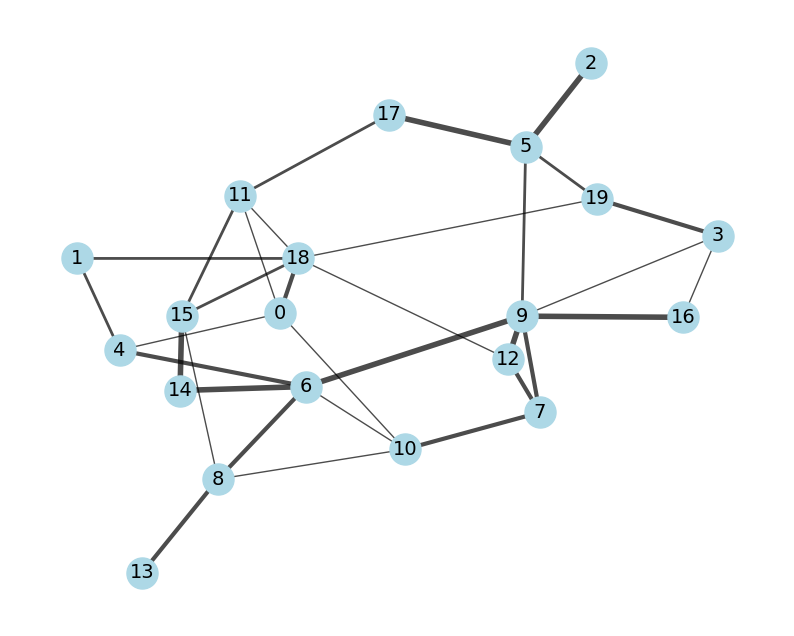
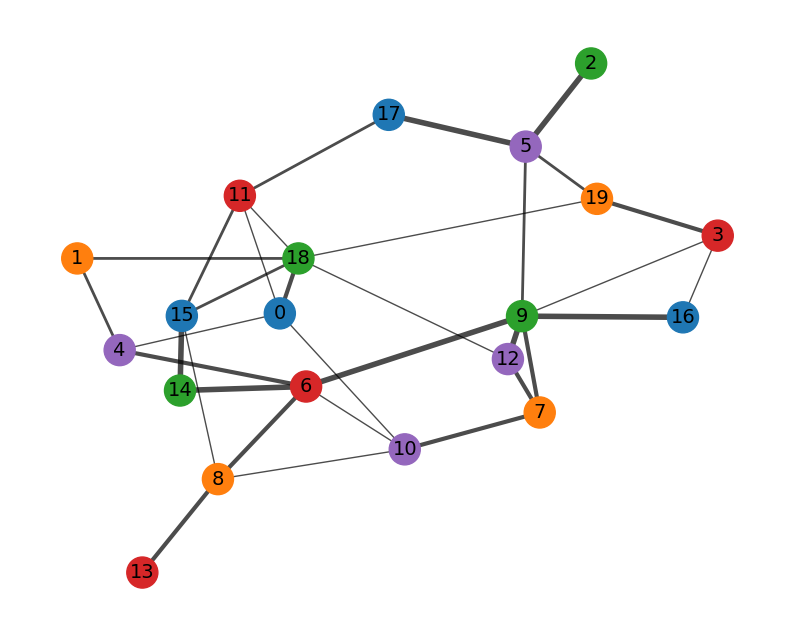
得られた結果をNetworkXで可視化してみると以下のようになります。 左側は、出席者同士の関係度合いをソーシャルグラフのように表現したもので、ノード番号が出席者の番号に対応しています。 今回扱った忘年会の配席問題は、エッジのつながったノード同士が同じ色にならないように、ノードを塗り分ける問題とも解釈することもできます。 右側は、最適化計算で割り当てられたテーブル毎にノードの色を塗り分けたもので、上手く色分けされた様子が確認できるかと思います。

出席者同士の関係度合いを表すグラフ

さいごに

この記事では、二次までの非線形な整数計画問題や混合整数計画問題を扱う場合、PyomoとSCIPを使い、まずは非線形の定式のまま厳密解法を実装してみるのが良いと主張してきました。 それでもし難あった場合も、 PyomoとSCIPはMILPにも対応しているので、線形の式に帰着させて解くアプローチに移りやすいかと思います。 それでも計算時間がかかったり、線形の式に変形するのが難解な場合には、近似解法の出番と考えています。

また、実務で組合せ最適化を扱う場合、適用業務の都合で制約条件の追加など式の見直しに迫られることも多く、中には線形だったのに二次式になってしまうケースもあります。 そういった恐れのある問題であれば、差し当たって線形な整数計画問題や混合整数計画問題であっても、予めPyomoとSCIPで実装して備えておくのが安全と考えます。

ただし以上のような優先順位は、非線形といっても二次までの議論であり、二次以外の非線形な問題の場合には、はなから近似解法を選択する方が良いかと思います。 但し書きで締めくくってしまいましたが、この記事がPyomoとSCIPを試すきっかけになれば幸いです！

*1:更に細分化した呼び方として、近似性能を保証するものを近似解法、保証しないものを発見的解法とする向きもありますが、この記事ではまとめて近似解法と呼んでいます。

*2:pythonのライブラリとして提供されており、そのライブラリの記法に沿って式をコーディングすると、最適化計算用のファイルに変換してくれるもの

*3:モデラ―から最適化計算用のファイルを受け取り、求解計算を実行して、解をモデラーに返却してくれるもの

*4:混合整数線形計画問題（MILP - Mixed Integer linear Programming）

*5:二次問題までの対応可否を記載しています

*6:2024/12時点