地域メッシュ計算ロジック詳解：緯度経度⇔コード相互変換をPythonで実装してみた

はじめに

NTTドコモデータプラットフォーム部の中村光宏と申します。
この記事では地理的情報のデータを分析する際に重要な「地域メッシュコード」について、定義やその計算⽅法を解説します。地域メッシュコードを⼿軽に扱うなら jismesh ライブラリ等便利なものもありますが、⼤規模処理の⾼速化やデバッグのためにロジックを理解しておく必要があります。メッシュコードの定義や計算方法に関しては、まとまった記事が少なく、LLMに質問しても正確な回答が得られにくい状況ですので、本記事のコードやまとめが地域メッシュを扱う際の参考になれば幸いです。

なお、本記事の掲載の取組については、⽀援メンバーであるAMBL株式会社の押切翔さんに詳細検討・実装を進めてもらっており、以下は、押切さんに執筆いただいています。

本記事では、例としてドコモ本社が位置する山王パークタワー代表地点の緯度経度を用います。

緯度：35.673139度
経度：139.740667度

はじめに
地域メッシュ
- 概要
- 定義
メッシュコード
Pythonによる実装
- 緯度経度からメッシュコードを求める関数
- メッシュコードから緯度経度を求める関数
最後に
参考資料

地域メッシュ

概要

「地域メッシュ」とは、日本全国の地理的な位置情報を、緯度と経度を基に格子状に分割したものです。これは総務省統計局が定めた統一基準に基づいており、国土全体を一定の大きさのメッシュに分割しています。それぞれのメッシュには「メッシュコード」と呼ばれる一意のコードが割り当てられ、このコードによって位置情報が管理されています。

地域メッシュを活用する最大のメリットは、位置情報の管理やデータ分析を定量的かつ効率的に行える点です。
例えば、以下のような様々な分野で活用されています。

人口統計データの集計: 特定のメッシュ内の人口密度や世帯構成を正確に把握する
災害対策・防災計画: 災害発生時の被害状況をメッシュ単位で迅速に分析し、対応計画を策定する
都市計画・マーケティング: 店舗の出店計画や交通量の分析など、地域に関する詳細な情報を効率的に取得する

さらに重要な利点として、地域メッシュが全国で統一された恒久的な規格である点が挙げられます。市町村などの行政区分は合併や境界変更によって時とともに変化することがありますが、地域メッシュの規格は変わりません。これにより、異なる地域間での正確な比較や、長期間にわたる時系列でのデータ比較・分析が容易に行えるという大きな強みがあります。総務省による国勢調査の集計結果も地域メッシュを用いて提供されています。（地域メッシュ統計）

定義

地域メッシュは北緯20度から46度、東経122度から154度までの日本全域にわたる範囲で設定されます。約80㎞四方の第1次地域区画（1次メッシュ）を基準に、以下のような階層構造で分割されます。

表1: 地域メッシュの階層構造

名称	本記事内での名称	大きさの目安	間隔（緯度、経度）	分割方法
第1次地域区画	1次メッシュ	約80km四方	$40'、60'$
第2次地域区画	2次メッシュ	約10km四方	$5'、7'30''$	1次メッシュを $8 \times 8$ 分割
第3次地域区画(基準地域メッシュ)	3次メッシュ	約1km四方	$30''、45''$	2次メッシュを $10 \times 10$ 分割
2分の1地域メッシュ	4次メッシュ	約500m四方	$15''、22.5''$	3次メッシュを $2 \times 2$ 分割
4分の1地域メッシュ	5次メッシュ	約250m四方	$7.5''、11.25''$	4次メッシュを $2 \times 2$ 分割
8分の1地域メッシュ	6次メッシュ	約125m四方	$3.75''、5.625''$	5次メッシュを $2 \times 2$ 分割

注：角度の度分秒（六十進法）表記
$1^\circ$ （度） $= 60'$ （分角） $= 3600''$ （秒角）
例えば、ドコモ本社である山王パークタワーの緯度経度を六十進法で表すと、
緯度： $35^\circ 40' 23.3''$ 、経度： $139^\circ 44' 26.4''$ となります。
余談ですが、天文学では恒星の位置や運動を、度分秒表記で表すことが一般的で、何ミリ秒角といった非常に小さな単位も使われます。

図1は、日本地図に青線で示した1次メッシュを重ねたものです。県境といった行政区画とは独立して設定されていることが一目でわかります。
ちなみに、面積の小さい香川県と大阪府は2つの1次メッシュ内に収まっていますが、それに次ぐ大きさの東京都は島が多いため、10を超える1次メッシュにまたがっています。

※メッシュに関する注意
表では「約1km四方」などの大きさの目安を示しましたが、地域メッシュは距離ではなく「緯度経度（角度）」に基づいて区画されています。地球は球体であるため、高緯度（北）に行くほど経線同士の間隔は狭くなります。そのため、同じ次数のメッシュであっても、北に行くほど東西の幅（実際の距離）は狭くなり、面積も小さくなる点には注意が必要です。

メッシュコード

さて、地域メッシュについての定義を理解したところで、次にメッシュコードを説明します。これは、各メッシュに割り当てられた一意の識別子（コード）であり、緯度経度からメッシュを特定したり、逆にメッシュコードからその範囲の緯度経度を求めたりするために使われます。

メッシュコードは、メッシュの南西端を基準に緯度経度を基にして算出されます。 4桁の数で表現される1次メッシュをもとに、2次メッシュ以降は桁を追加して表現されます。例えば、山王パークタワーの位置するメッシュは、1次メッシュコードで「5339」、6次メッシュコードまで計算すると、「53394509341」となります。

計算の全体像

では、実際にメッシュコードをどのように算出するのか、その計算手順を説明します。詳細な計算に入る前に、メッシュコード計算のポイントを3つにまとめます。

入れ子構造
大きな区画（1次）の中に中くらいの区画（2次）があり、その中にさらに小さな区画（3次...）があるという階層構造になっています。
緯度経度 $\rightarrow$ メッシュコード
ある座標が、区画内の何番目のマス目にあるかを計算します。単位変換して整数部を取り出し、残った余り（小数点以下）を次のレベルの計算に引き継ぎます。
メッシュコード $\rightarrow$ 緯度経度
メッシュコードは、基準点からの「ズレ」を表します。各レベルの区画の幅・高さにメッシュコードの数字を掛け合わせ、それらを足し合わせていくことで座標（南西端）を復元します。

緯度経度からメッシュコードを求める

では、実際にメッシュコードを順に求めていきましょう。計算のカギは、単位の変換と整数部の取り出しの繰り返しです。

1次メッシュコードの算出方法

1次メッシュコードは、緯度0度（赤道）、経度100度を基準点（0000）として、4桁の数字で表現されます。

上2桁（緯度方向）: 緯度を40分（40/60度）で割ったときの整数部分
下2桁（経度方向）: 経度から100を引いたときの整数部分

例えば、山王パークタワーでは、

緯度: $35.673139 / (40/60) = 53.5097... \rightarrow 53$
経度: $139.740667-100 = 39.7406... \rightarrow 39$

よって、1次メッシュコードは「5339」となります。

2次メッシュコードの算出方法

2次メッシュは、1次メッシュの区画を縦横それぞれ8分割して作られます。図2は、1次メッシュ「5339」の中に2次メッシュを重ねた地図です。太い赤枠が1次メッシュ、細い赤枠が2次メッシュを示しています。
2次メッシュコードは、1次メッシュコードの計算で生じた余り（小数点以下）を、8倍して整数部分を取り出すことで求められます。これは、1次メッシュの大きさを8分割した単位系への変換を意味します。ここで8倍するのは、緯度方向には、 $40'/5'$ 、経度方向には、 $60'/7'30''$ の比率に基づいています。

上1桁: 1次メッシュ計算の余りを8倍した整数部分
下1桁: 1次メッシュ計算の余りを8倍した整数部分

例（山王パークタワー）:

緯度: $53.5097...$ の余り $0.5097... \times 8 = 4.077... \rightarrow 4$
経度: $39.7406...$ の余り $0.7406... \times 8 = 5.925... \rightarrow 5$

これらを続けて、2次メッシュコードは「5339-45」となります。図2の[45]の区画が山王パークタワーの位置する2次メッシュです。

3次メッシュコードの算出方法

3次メッシュ（基準地域メッシュ）は、2次メッシュの区画を縦横それぞれ10分割して作られます。 2次メッシュコードの計算と似ていて、余りを10倍します。 10倍の理由は、緯度方向には、 $5'/30''$ 、経度方向には、 $7'30''/45''$ の比率に基づいています。

上1桁: 2次メッシュ計算の余りを10倍した整数部分
下1桁: 2次メッシュ計算の余りを10倍した整数部分

例（山王パークタワー）:

緯度: $4.077...$ の余り $0.077... \times 10 = 0.77... \rightarrow 0$
経度: $5.925...$ の余り $0.925... \times 10 = 9.25... \rightarrow 9$

これらを続けて、3次メッシュコードは「5339-45-09」となります。

図3は、2次メッシュ「5339-45」の中に3次メッシュを重ねた地図です。 [09]の区画が山王パークタワーの位置する3次メッシュです。

4次・5次・6次メッシュコードの算出方法

4次メッシュ以降は、前のメッシュを縦横それぞれ2分割して細分化していきます。計算方法は、前のメッシュコード計算での余りを2倍し、その整数部分（0または1）を使って以下のルールで数字（1〜4）を割り当てます。 3次メッシュコードまでは0が基準でしたが、4次メッシュコード以降は1から始まる点に注意してください。

表2: 4次メッシュ以降のコードの割り当て

コード	位置	緯度方向	経度方向	計算式
1	南西 (左下)	0 (南)	0 (西)	$0 \times 2 + 0 + 1$
2	南東 (右下)	0 (南)	1 (東)	$0 \times 2 + 1 + 1$
3	北西 (左上)	1 (北)	0 (西)	$1 \times 2 + 0 + 1$
4	北東 (右上)	1 (北)	1 (東)	$1 \times 2 + 1 + 1$

図4は、3次メッシュ「5339-45-09」の中に4次メッシュを重ねた地図です。 [3]の区画が山王パークタワーの位置する4次メッシュです。 4次以降は、この図のように4分割された区画のどこに位置するかで数字が決まります。

4次メッシュ:

緯度: $0.77...$ の余り $0.77... \times 2 = 1.55... \rightarrow 1$ (北側)
経度: $9.25...$ の余り $0.25... \times 2 = 0.50... \rightarrow 0$ (西側)
メッシュコード: $1 \times 2 + 0 + 1 = \mathbf{3}$

5次メッシュ:

緯度: $1.55...$ の余り $0.55... \times 2 = 1.10... \rightarrow 1$ （北側）
経度: $0.50...$ の余り $0.50... \times 2 = 1.01... \rightarrow 1$ （東側）
メッシュコード: $1 \times 2 + 1 + 1 = \mathbf{4}$

6次メッシュ:

緯度: $1.10...$ の余り $0.10... \times 2 = 0.21... \rightarrow 0$ （南側）
経度: $1.01...$ の余り $0.01... \times 2 = 0.02... \rightarrow 0$ （西側）
メッシュコード: $0 \times 2 + 0 + 1 = \mathbf{1}$

最後にすべてをつなげると、「5339-45-09-3-4-1」となります。

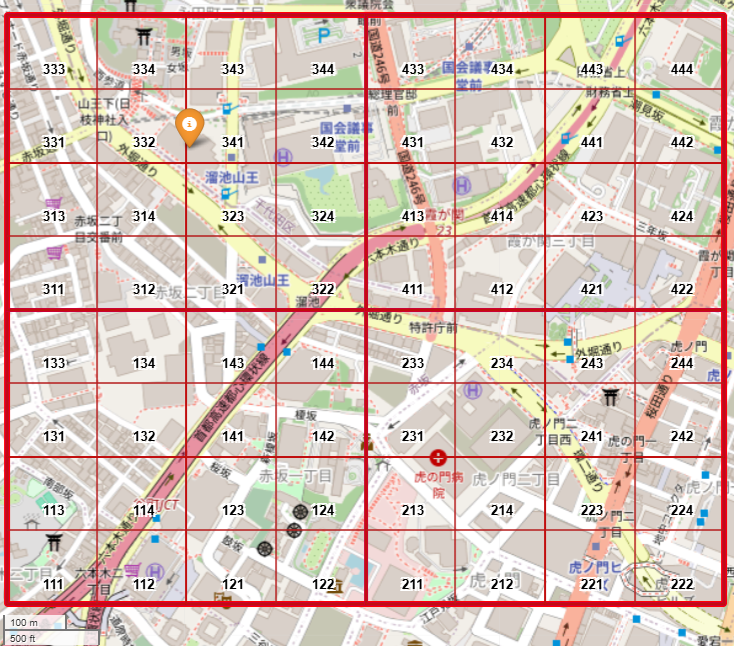
図5は、3次メッシュ「5339-45-09」の中に4次・5次・6次メッシュを重ねた地図です。 [341]の区画が山王パークタワーの位置する6次メッシュです。
これで、緯度経度が与えられたときに、その位置する各レベルのメッシュをメッシュコードで表現できるようになりました。

メッシュコードから緯度経度を求める

続いて、メッシュコードからそのメッシュの基準点となる緯度経度を求める方法です。 1次メッシュから順に基準点（南西端）を求め、そこから各レベルの緯度方向のズレと経度方向のズレを加算していくことで算出します。

基準点を決める
まず、1次メッシュコード（上4桁）から、そのメッシュの南西端（基準点）の緯度経度を求めます。
位置をずらしていく
続く桁（2次、3次...）を見るたびに、そのメッシュの大きさを計算し、何区画分だけ東や北にずれているかを足し合わせていきます。
範囲を確定する
最後に、算出した南西端にそのメッシュ自体の大きさを足すことで、北東端の座標も求められます。

算出する座標は、そのメッシュの南西端（左下）の緯度経度です。 1次メッシュの基準点を出発点とし、各桁の数字が示す「ズレ」を度に変換して順次足していくことで算出します。
ここでは、先ほど求めた6次メッシュコード「5339-45-09-3-4-1」から、6次メッシュの基準点（南西端）の座標を復元していきます。

1次メッシュの基準点を求める

上2桁が緯度、下2桁が経度のベースとなります。

緯度: $53 \times (2/3)^\circ \approx 35.3333...^\circ$
経度: $39 + 100^\circ = 139^\circ$

これが計算のスタート地点です。

2次・3次メッシュの幅を加算する

2次メッシュ以降は、「数字 $\times$ メッシュの大きさ」を足していきます。

表3: 2次・3次メッシュの大きさ

次数	大きさ (緯度)	大きさ (経度)	コード(緯-経)
2次	$5' = (1/12)^\circ$	$7'30'' = (1/8)^\circ$	4 5
3次	$30'' = (1/120)^\circ$	$45'' = (1/80)^\circ$	0 9

緯度: 1次メッシュの基準点に、 $4 \times (1/12)^\circ$ と $0 \times (1/120)^\circ$ を足す。
経度: 1次メッシュの基準点に、 $5 \times (1/8)^\circ$ と $9 \times (1/80)^\circ$ を足す。

4次以降のメッシュ幅を加算する

4次メッシュ以降（1〜4）は、メッシュコードの数字によって足すべき値が決まります。 3・4は北側なので緯度にメッシュの大きさを足す、2・4は東側なので経度にメッシュの大きさを足すというルールです。

表4: 4次メッシュ以降の大きさと判定

次数	大きさ (緯度)	大きさ (経度)	コード	判定 (緯度/経度)
4次	$15'' = (1/240)^\circ$	$22.5'' = (1/160)^\circ$	3	北(+1) / 西(+0)
5次	$7.5'' = (1/480)^\circ$	$11.25'' = (1/320)^\circ$	4	北(+1) / 東(+1)
6次	$3.75'' = (1/960)^\circ$	$5.625'' = (1/640)^\circ$	1	南(+0) / 西(+0)

最終結果の確認

以上より、すべての「ズレ」を合計すると、以下のように6次メッシュコード「5339-45-09-3-4-1」の基準点の座標が求まります。

緯度: $53 \times (2/3)^\circ + 4 \times (1/12)^\circ + 0 \times (1/120)^\circ + 1 \times (1/240)^\circ + 1 \times (1/480)^\circ + 0 \times (1/960)^\circ = 35.6729166...^\circ$

経度: $139.0^\circ + 5 \times (1/8)^\circ + 9 \times (1/80)^\circ + 0 \times (1/160)^\circ + 1 \times (1/320)^\circ + 0 \times (1/640)^\circ = 139.740625^\circ$

北東端の座標は、いま算出された6次メッシュコードの基準点（南西端）に、6次メッシュの大きさ（緯度方向: $3.75''$ 、経度方向: $5.625''$ ）を足すことで求めることができます。

Pythonによる実装

先の章で見たメッシュコードと緯度経度の変換をPythonで実装した例を以下に示します。学習用として可読性を優先してfloat型を使用していますが、厳密な境界判定が必要な場合はPython標準のDecimalモジュールの利用を検討してください。

緯度経度からメッシュコードを求める関数

def latlon_to_meshcode(lat, lon, level):
    """
    緯度経度から地域メッシュコードを計算する関数
    
    Args:
        lat (float): 緯度
        lon (float): 経度
        level (int): 求める次数 (1〜6)
    
    Returns:
        str: メッシュコード
    """
    # --- 1次メッシュ ---
    # 緯度を1.5倍、経度から100を引く
    t_lat = lat * 1.5
    t_lon = lon - 100.0

    m1_lat = int(t_lat)
    m1_lon = int(t_lon)
    
    # コードリスト作成
    mesh_code = [f"{m1_lat}{m1_lon:02}"]
    
    if level == 1:
        return "".join(mesh_code)

    # --- 2次メッシュ ---
    # 1次メッシュの残差(小数点以下)を8倍する
    # 1次メッシュ単位を2次メッシュ単位に変換する
    t_lat = (t_lat - m1_lat) * 8
    t_lon = (t_lon - m1_lon) * 8
    
    m2_lat = int(t_lat)
    m2_lon = int(t_lon)
    mesh_code.append(f"{m2_lat}{m2_lon}")

    if level == 2:
        return "".join(mesh_code)

    # --- 3次メッシュ ---
    # 2次メッシュの残差を10倍する
    t_lat = (t_lat - m2_lat) * 10
    t_lon = (t_lon - m2_lon) * 10
    
    m3_lat = int(t_lat)
    m3_lon = int(t_lon)
    mesh_code.append(f"{m3_lat}{m3_lon}")

    if level == 3:
        return "".join(mesh_code)

    # --- 4次〜6次メッシュ ---
    # ここからは共通ルール：残差を2倍して 1〜4 を割り当てる
    
    # 次のループ計算のために、3次メッシュの整数部を基準として保存
    curr_lat_int = m3_lat
    curr_lon_int = m3_lon

    for _ in range(4, level + 1):
        # 前のメッシュの残差を2倍する
        t_lat = (t_lat - curr_lat_int) * 2
        t_lon = (t_lon - curr_lon_int) * 2
        
        curr_lat_int = int(t_lat) # 0 or 1 (北 or 南)
        curr_lon_int = int(t_lon) # 0 or 1 (西 or 東)
        
        # コード計算: 緯度bit * 2 + 経度bit + 1
        # 0,0->1(SW), 0,1->2(SE), 1,0->3(NW), 1,1->4(NE)
        code = curr_lat_int * 2 + curr_lon_int + 1
        mesh_code.append(str(code))

    return "".join(mesh_code)

メッシュコードから緯度経度を求める関数

def meshcode_to_latlon(mesh_code):
    """
    メッシュコードから、その区画の4隅と中心の座標を計算して返します。
    
    Args:
        mesh_code (str): 地域メッシュコード
    
    Returns:
        dict: {
            'sw': (lat, lon),  # 南西（基準点） 
            'se': (lat, lon),  # 南東 
            'nw': (lat, lon),  # 北西 
            'ne': (lat, lon),  # 北東 
            'center': (lat, lon) # 中心点
        }
    """

    # メッシュコードの桁数
    length = len(mesh_code) 

    # --- 1次メッシュ (4桁) ---
    # 基準となるサイズ（1次メッシュの幅と高さ）
    lat_delta = 2.0 / 3.0  # 40分 = 40/60度
    lon_delta  = 1.0       # 1度
    
    # 1次メッシュの南西端（基準）を計算
    # 緯度: 上2桁 * 2/3
    # 経度: 下2桁 + 100
    lat = int(mesh_code[0:2]) * lat_delta
    lon = int(mesh_code[2:4]) + 100.0

    if length <= 4:
        return _make_result(lat, lon, lat_delta, lon_delta)

    # --- 2次メッシュ (6桁) ---
    # 1次メッシュを 8等分 (0~7)
    lat_delta /= 8.0
    lon_delta  /= 8.0
    
    lat += int(mesh_code[4]) * lat_delta
    lon += int(mesh_code[5]) * lon_delta

    if length <= 6:
        return _make_result(lat, lon, lat_delta, lon_delta)

    # --- 3次メッシュ (8桁) ---
    # 2次メッシュを 10等分 (0~9)
    lat_delta /= 10.0
    lon_delta  /= 10.0
    
    lat += int(mesh_code[6]) * lat_delta
    lon += int(mesh_code[7]) * lon_delta

    if length <= 8:
        return _make_result(lat, lon, lat_delta, lon_delta)

    # --- 4次・5次・6次メッシュ (9桁以降) ---
    # 前のメッシュを 2等分 し、1〜4 の数字で位置を特定します。
    # 1:南西, 2:南東, 3:北西, 4:北東
    
    for i in range(8, length):
        lat_delta /= 2.0
        lon_delta  /= 2.0
        
        mesh_code_i = int(mesh_code[i])
        
        # 北側 (3 or 4) なら緯度をプラス
        if mesh_code_i in [3, 4]:
            lat += lat_delta
        
        # 東側 (2 or 4) なら経度をプラス
        if mesh_code_i in [2, 4]:
            lon += lon_delta

    return _make_result(lat, lon, lat_delta, lon_delta)

def _make_result(sw_lat, sw_lon, lat_delta, lon_delta):
    """計算された南西端とサイズから、四隅と中心を整理して返す"""
    return {
        'sw': (sw_lat, sw_lon),
        'se': (sw_lat, sw_lon + lon_delta),
        'nw': (sw_lat + lat_delta, sw_lon),
        'ne': (sw_lat + lat_delta, sw_lon + lon_delta),
        'center': (sw_lat + lat_delta / 2, sw_lon + lon_delta / 2)
    }

コードの解説：4次メッシュ以降のロジック

3次メッシュまでは「数字＝何個分ずらすか」という単純な掛け算でしたが、4次メッシュ以降（分割地域メッシュ）は少し特殊です。数字（1〜4）は以下のように割り当てられています。

表5: 4次メッシュ以降の区画番号の割り当てと緯度経度の加算ルール

コード	位置	緯度(Lat)	経度(Lon)
1	南西 (左下)	そのまま	そのまま
2	南東 (右下)	そのまま	足す
3	北西 (左上)	足す	そのまま
4	北東 (右上)	足す	足す

コード内の以下の部分で、このロジックを判定しています。

# 北側 (3 or 4) なら緯度を足す
if mesh_code_i in [3, 4]:
    lat += lat_delta

# 東側 (2 or 4) なら経度を足す
if mesh_code_i in [2, 4]:
    lon += lon_delta

これにより、再帰的に細分化される4次以降のメッシュの位置も正しく計算することができます。

最後に

本記事では、地域メッシュのロジックについて定義に立ち返って解説しました。
メッシュコードを単なる11桁の数字の羅列として見るのではなく、そのコードが示す広さや位置関係を直感的にイメージできるようになると、解像度の上がった分析が可能になるはずです。この記事が皆様の地理データ分析の一助となれば幸いです。