NTTドコモR&Dの技術ブログです。

トップ > プログラミング > 【Python】意思決定支援のために手元で数理最適化を使ってみた話

【Python】意思決定支援のために手元で数理最適化を使ってみた話

プログラミング データ分析 アドベントカレンダー2023

はじめに

本記事はNTTドコモ Advent Calendar 2023の7日目の記事です。

こんにちは。NTTドコモサービスイノベーション部2年目の杉山です。
業務ではAI技術等のビジネス適用をしております。

入社してから2年目になりますが、たった2年の間にも社内におけるデータ活用は広がりを見せております。 データにあまり詳しくない人でも簡単に使えるAutoMLツールの台頭もあり、モデリングやモデルから出力されるスコアの活用はより身近なものになってきていると感じています。 そうなってくると研究開発チームとしてはスコアの算出だけではなく、その先の意思決定部分も含めた技術開発をすることで更になる価値創出につながり、最近では数理最適化技術を勉強しております。 Pythonで数理最適化ができるライブラリはいくつかありますが、本記事ではその中でも3種類のライブラリを手元で動かしてみましたので、その内容を紹介します。

忙しい方向け

  • Python上で数理最適化問題をモデリングできるライブラリを3種類 (PuLP、Python-MIP、pyscipopt) を使ってみた
  • 今回は厳密解が見つかる問題設定で、データサイズによる実行時間のスケールを比較
    • Python-MIPのライブラリが高速に動作する結果

数理最適化とは

数理最適化は与えられた条件下で目的を達成するために最適な解を計算する技術です。 ここでの最適とは主に目的関数と呼ばれる値を最大化もしくは最小化することを指します。 例えば、輸送コストを最小化にする配送問題や、利益を最大にするためにどの製品をどの工場で生産するかを決定する問題などは数理モデルに落とし込んで最適化することによって解決することができます。

オペレーションズ・リサーチ学会のページ(こちら)に数理最適化の分かりやすい活用例がありますので、引用させていただきます。

数理最適化は複数の問題に分類することができ、今回の実装例では整数計画問題を扱います。
1. 整数計画問題 (←今回の実装例はこれ)：後述する線形計画問題の中で変数の取る値を整数に制限したもの
2. 線形計画問題：目的関数が一次式として表され、制約条件も一次の等式 or 不等式で定義されているもの
3. 非線形計画問題：目的関数、制約条件の中で非線形なものが含まれれるもの
4. etc...

数理最適化問題の関係

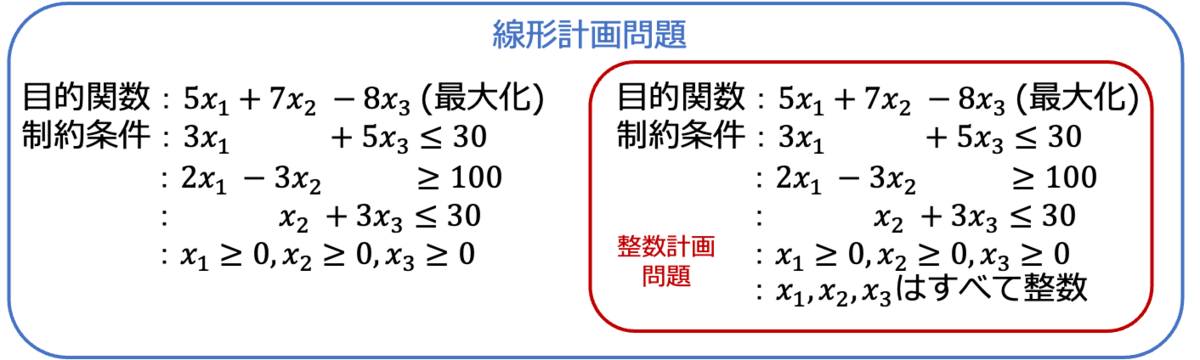
業務で扱っていく上で、数理最適化を実際のビジネスに落とし込む際には、何を最適化(最大/最小)したいのか、何を条件としているのかなどをしっかりとヒアリングすることが重要だと感じています。 要望を実際のモデルに落とし込んでいく、言語→数式の変換が開発者の腕の見せどころとなりそうです。

Pythonでの数理最適化

Pythonで数理最適化を実施するためには、2ステップ必要となります。 1. ライブラリ(モデラー)で数理モデルの作成 2. 作成した数理モデルをソルバーに入力して解を計算 Pythonで使えるモデラーはいくつかあり、ソルバーもそれぞれの用途に合わせていくつかあります。

今回使ったソルバーとモデラーの組み合わせは以下になります。

ソルバー/モデラー PuLP Python-MIP pyscipopt
CBC ◯ ◯
GLPK ◯
SCIP ◯ ◯

(SCIPは昨年商用利用が無償になりました)

他にはモデラーでは数値計算でよく使われるSciPy、非線形最適化問題の中でも凸最適化問題を解けるCVXOPT、多目的最適化を解くことができるPyomoなどがあります。また、ソルバーでは有償となるGurobiやCPLEXなどが有名となりますが、今回は使っていません。

Pythonを使ったコーディング

動作環境

  • Python 3.9.18

今回扱う最適化問題

今回はクーポン配信最適化を考えます。 各ユーザーの配信媒体ごとの反応率を元に、それぞれのユーザーにどの配信媒体で配信するかをを決定します。 実際のクーポン配信に近づけるため、クーポン配信の予算と各媒体で10%以上のユーザーに送付するといった制約を設けます。

\displaystyle \begin{array}{lll} \mathrm{Maximize} &\sum_{i \in I} \sum_{m \in M} \mathrm{S}_{i, m} \times x_{i, m}& \\ \mathrm{subject\ to}& \sum_{i \in I} \sum_{m \in M} u_m \times x_{i, m} \geq \mathrm{cost\_low}& & \\ &\sum_{i \in I} \sum_{m \in M} u_m \times x_{i, m} \leq \mathrm{cost\_up}& & \\ &\sum_{i \in I} x_{i, m} \geq 0.1 \times |I|& & \forall m \in M\\ &\sum_{m \in M} x_{i, m} = 1& & \forall i \in I\\ &x_{i, m} \in \{0, 1\}& & \forall i \in I, \forall m \in M \end{array}
  • S_{i, m}：ユーザー$i$に配信媒体$m$を配信したときの反応率
  • x_{i, m}：ユーザー$i$に配信媒体$m$を配信するかどうかの変数
  • u_m：配信媒体$m$の単価
  • I：ユーザーの集合
  • M：配信媒体の集合
  • \mathrm{cost_low}：クーポン配信の予算下限
  • \mathrm{cost_up}：クーポン配信の予算上限

PuLP

最も日本語記事が多く使いやすいライブラリです。 デフォルトではCBCのソルバーが使われますが、GLPK、SCIPやその他ソルバーもインストールすれば使えます。

↓PuLPのインストール

pip install pulp

↓GLPKのインストール

brew install glpk

モデリング

def pulp_opt(df, I, M, id_column, cost_range, unit_prices, sol='CBC'):
    # 最適化問題の初期化z
    problem = pulp.LpProblem(name='CouponDelivery',sense=pulp.LpMaximize)
    
    # 決定変数の初期化
    x = {}
    for i in I:
        for m in M:
            x[i,m] = pulp.LpVariable(name=f'x({i},{m})',cat='Binary')

    # 各種データの辞書化
    S = df.melt(id_vars=id_column, value_vars=M, var_name='dm', value_name='score').set_index([id_column, 'dm'])['score'].to_dict()
    u = dict(zip(M, unit_prices))
    
    # 最大化問題
    problem += pulp.lpSum(S[i, m] * x[i,m] for i in I for m in M)
        
    # 予算制約
    problem += pulp.lpSum(x[i,m] * u[m] for i in I for m in M) >= cost_range[0] # コスト下限
    problem += pulp.lpSum(x[i,m] * u[m] for i in I for m in M) <= cost_range[1] # コスト上限

    # 配信数の制限
    for m in M:
        problem += pulp.lpSum(x[i,m] for i in I) >= len(I)*0.1 # 配信は全体の10%以上に送る

    # 各ユーザーはどれか1媒体に送付
    for i in I:
        problem += pulp.lpSum(x[i,m] for m in M) == 1
    
    # ソルバーの選択
    solver = pulp.COIN_CMD() # CBC
    # solver = pulp.GLPK() # GLPK
    # solver = pulp.SCIP() # SCIP
    
    status = problem.solve(solver)
    return pd.DataFrame([[x[i,m].value() for m in M] for i in I], columns=M)

Python-MIP

PuLPと同じくデフォルトではCBCのソルバーが使われますが、その他のソルバーは使えないようです。 PuLPとの大きな違いはPuLPはファイルベースでソルバーとやり取りしていることに対し、Python-MIPはCFFIを使ってやり取りしているので高速に動作するという点です。

↓Python-MIPのインストール

pip install mip

自前の環境ではcbcのソルバーをインストール必要があるので、こちらを参考にインストールしました。

モデリング

def mip_opt(df, I, M, id_column, cost_range, unit_prices):
    # 最適化問題の初期化
    model = mip.Model(name='CouponDelivery')
    
    # 決定変数の初期化
    x = {}
    for i in I:
        for m in M:
            x[i,m] = model.add_var(name=f'x({i},{m})',var_type=mip.BINARY)

    # 各種データの辞書化
    S = df.melt(id_vars=id_column, value_vars=M, var_name='dm', value_name='score').set_index([id_column, 'dm'])['score'].to_dict()
    u = dict(zip(M, unit_prices))
    
    # 最大化問題
    model.objective = mip.maximize(mip.xsum(S[i, m] * x[i,m] for i in I for m in M))
        
    # 予算制約
    model.add_constr(
        mip.xsum(x[i,m] * u[m] for i in I for m in M) >= cost_range[0]
    )
    model.add_constr(
        mip.xsum(x[i,m] * u[m] for i in I for m in M) <= cost_range[1]
    )

    # 配信数の制限
    for m in M:
        model.add_constr(
            mip.xsum(x[i,m] for i in I) >= len(I)*0.1
        )

    # 各ユーザーはどれか1媒体に送付
    for i in I:
        model.add_constr(
            mip.xsum(x[i,m] for m in M) == 1
        )

    model.optimize()
    return pd.DataFrame([[x[i,m].x for m in M] for i in I], columns=M)

pyscipopt

pyscipoptはSCIPのPythonインターフェースです。 SCIPはCBCより高速に動くソルバーとなり、そのSCIPのPythonインターフェースがpyscipoptとなります。 こちらはまだ日本語記事は多くはないです。

↓pyscipoptのインストール

pip install pyscipopt

モデリング

def pyscipopt_opt(df, I, M, id_column, cost_range, unit_prices):
    # 最適化問題の初期化
    model = Model(problemName='CouponDelivery')
    
    # 決定変数の初期化
    x = {}
    for i in I:
        for m in M:
            x[i,m] = model.addVar(name=f'x({i},{m})',vtype='B')

    # 各種データの辞書化
    S = df.melt(id_vars=id_column, value_vars=M, var_name='dm', value_name='score').set_index([id_column, 'dm'])['score'].to_dict()
    u = dict(zip(M, unit_prices))
    
    # 最大化問題
    model.setObjective(
        quicksum(S[i, m] * x[i,m] for i in I for m in M),
        sense='maximize'
    )
        
    # 予算制約
    model.addCons(
        quicksum(x[i,m] * u[m] for i in I for m in M) >= cost_range[0]
    )
    model.addCons(
        quicksum(x[i,m] * u[m] for i in I for m in M) <= cost_range[1]
    )

    # 配信数の制限
    for m in M:
        model.addCons(
            quicksum(x[i,m] for i in I) >= len(I)*0.1
        )

    # 各ユーザーはどれか1媒体に送付
    for i in I:
        model.addCons(
            quicksum(x[i,m] for m in M) == 1
        )

    model.optimize()
    return pd.DataFrame([[model.getVal(x[i, m]) for m in M] for i in I], columns=M)

実装してみて

実装してみてPuLPとそれ以外のライブラリとの大きな違いは目的関数や制約の記述方法だと感じました。PuLPでは目的関数も制約のどちらも+=で記述しますが、Python-MIPやpyscipoptでは目的関数はobjective、制約はconstrを明記して定義することができます。また、今回のコードは元々PuLPで実装したものを他に移植したので使いませんでしたが、Python-MIPはベクトルを使った記述もできるようです。

実行時間の比較

今回はそれぞれの実行時間を比較するために以下の条件でデータを作成して検証しました。

  • ユーザー数：100、1,000、2,000
  • 媒体数：3
  • 比較するモデラー/ソルバー：PuLP/CBC、PuLP/GLPK、PuLP/SCIP、Python-MIP/CBC、pyscipopt/SCIP

実行結果はこちらになります。

ソルバーにSCIPを使うと高速に動作すると思っていましたが、モデラーがPulP、puscipoptのどちらで使ったとしてもかなり実行時間がかかっています。SCIP自体はpyscipoptのライブラリにくっついてきたものを使っているので別途SCIPのみをインストールすることで改善するかもしれないです。

SCIPを除外して更にユーザー数を大きくして実行時間を比較してみます。

  • ユーザー数：10,000、50,000、100,000
  • 媒体数：3
  • 比較するモデラー/ソルバー：PuLP/CBC、PuLP/GLPK、Python-MIP/CBC

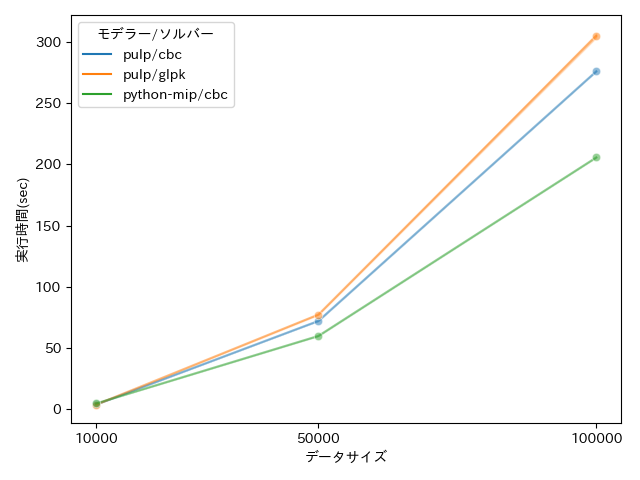
今回はPython-MIPのライブラリがもっとも高速に動作することが分かります。100,000のユーザー数の場合PuLPは1GBのmpsファイルを作成しており、作成するのに1分以上かかっていました。 Python-MIPはmpsファイルを作成せずに直接ソルバーに渡しているのでその違いが実行時間の違いになっているみたいです。(こちらの記事)

またどちらも計算時間はデータサイズに対して線形ではないように見えるので、データサイズが大きくなったときには計算時間がどうなるかは気になるところです。

まとめ

今回はPythonで使える数理最適化モデラー/ソルバーを使って手元で検証した内容を紹介いたしました。 今回は使いませんでしたが、有償となるGurobi等のソルバーはかなり高速で動作するようですので、どの程度の違いがあって問題サイズのスケーリングも気になるので業務で使う機会があれば比較してみたいと思います。

参考文献