TL;DR
この記事では,Causal Discovery Toolbox(cdt)を用いて観測データから因果関係を簡単に解析する方法を紹介します.cdtは,Pythonで利用可能なツールで複数の因果分析モデルとアルゴリズムを提供しデータから因果関係を推定し視覚化することができます.特に,PCアルゴリズム,GES,LiNGAMなどの主要なアルゴリズムを使用した因果探索の手順とサンプルコードを提供し,それぞれの性能評価も行います.
はじめに
本記事はNTTドコモ Advent Calendar 2023 22日目の記事です. こんにちは,サービスイノベーション部の阿座上です. 普段は社内データの分析および機械学習関連の研究開発に従事しています.
Causal Discovery Toolbox(cdt)は,因果探索と呼ばれるデータから因果関係*1を推定し因果構造を解析する技術を扱えるPythonツールです.今回は,簡単に因果探索を行うことができるCausal Discovery Toolboxを使って,観測データから因果関係を解析してみようと思います. 私の観測範囲ですとCausal Discovery Toolboxに触れた記事が見つからなかったので,この機会にご紹介させていただこうと思います.
因果探索のためのモデルやアルゴリズムは多く発表されていますが,どれもイチから始めようとするとそれぞれのツール実行のために個別に環境構築が必要になったり,使い方の理解が必要になったりと,実行コストが高くなりがちです. cdtでは主要な因果探索モデルを一つのツールで試すことができるため,非常に簡単に因果探索を試すことができます.
本記事では,cdtの紹介からセットアップ方法,利用可能なモデルの詳細な説明,そしてPCアルゴリズムによる因果分析の説明と詳細なサンプルコードを提供します.また,因果探索についてもさらりと説明します.
公式リンク github.com
因果探索とは
因果探索(Causal Discovery)は,データから因果関係を理解し,変数間の因果関係を明らかにする手法です.通常,因果関係を推定するために統計的手法や機械学習アルゴリズムが使用されます.因果探索により以下のような疑問を解くヒントを得ることができます.
- どの変数が他の変数に影響を与えているか?
- 結果に対してどの変数が原因になっているのか?
- 変数間の因果関係は直接的なものなのか,間接的なものなのか?
結果を引き起こした原因を明らかにし因果関係を特定することは,科学的な研究や意思決定プロセスにおいて非常に重要です. 因果探索はまだまだ発展途上の技術ですが,医療診断,経済学,社会科学,信頼性工学など様々な領域で応用が期待されており,cdtはデータから因果関係を解明するためのツールとして非常に役立ちます.
Causal Discovery Toolbox(cdt)

Causal Discovery Toolbox(cdt)は,因果関係の解析と因果グラフの推定を行うためのPythonライブラリです. cdtでは多くの因果分析モデルとアルゴリズムを提供し,データから因果関係を推定し,因果関係のグラフをモデル化することができます. 主要な機能は以下のものがあります.
- 因果関係の推定
- 異なる因果関係モデルを提供し,データから変数間の因果関係を推定します
- これにより,特定の変数が他の変数にどのように影響を与えているかを理解できます
- 因果関係のグラフ構築
- 因果関係のグラフを構築するためのツールを提供します
- これにより,変数間の因果関係を視覚化し,因果関係の構造を理解できます
- グラフ構造の可視化にはNetworkX*2が利用されます
- 因果関係の検定
- 異なる統計的検定手法を使用して因果関係を検定します
- これにより,因果関係の統計的有意性を評価できます
環境構築
利用のためにはPython 3.5以上にすることと,下記のインストールも必要となります.
numpy scipy scikit-learn joblib pandas networkx tqdm GPUtil statsmodels requests torch
また,cdtのパッケージ内ではPyTorchを利用するため,お手元のハードウェアに適したPyTorchバージョンをインストールしてください.
PyTorchのバーションを調べるにはこちらから pytorch.org
なお,筆者はDockerコンテナを立てて利用することをおすすめします. 理由としては,色々なライブラリのインストールによって依存関係の問題でコードが動かなくなったり,手元の環境が汚れてしまうことを防ぐためです. 今回は公式で用意されているDockerイメージを利用して環境構築を行います.
docker pull divkal/nv-cdt-py3.6:0.5.17
ここでは,TAG 0.5.17のものを利用しました.また,公式が用意しているGPU用のDockerイメージは3.6系までのものしかありませんので,最新のPythonバージョンを利用したい場合はご自身でDockerfileを用意するのも良いと思います.
docker pullが完了したらコンテナを立ち上げます.
docker run -it --runtime=nvidia divkal/nv-cdt-py3.6:0.5.17
docker runのコマンドもご自身の環境に合わせてカスタマイズしてください.
コンテナが立ち上がったら,pip listで必要なライブラリがインストールされているか確認します.
root@10cff8432c97:/workspace# pip list Package Version ----------------------------- --------------- ... GPUtil 1.4.0 joblib 0.13.2 networkx 2.4 numpy 1.16.3 pandas 0.24.2 requests 2.22.0 scikit-learn 0.22.1 scipy 1.4.1 statsmodels 0.11.0 tqdm 4.31.1 torch 1.1.0a0+828a6a3 ...
きちんとインストールされていれば,環境構築は終了です. (割愛していますがもっといろんなものがインストールされています)
利用できるアルゴリズム
cdtではさまざまな因果関係モデルが提供されており,データの特性に合わせて最適なモデルを選択できます.以下にcdtで扱える主要なモデルについて紹介します.
1.PCアルゴリズム (PC)
条件付き独立性に基づいて因果グラフを推定する.条件付き独立性テストを通じて変数間の依存関係を探索し,有向非循環グラフ(DAG)*3を生成する.
2.CAM (Causal addtive model)
因果的加法モデル(CAM)を導入し,変数の順序を特定する新しいアルゴリズムと罰則化回帰を組み合わせて,高次元データにおける因果関係のモデリングと発見が可能.
3.CGNN (Causal Generative Neural Networks)
因果関係をモデル化するための生成型ニューラルネットワーク.(Graph Neural NetworkのGNNではない)
4.GES (Greedy Equivalence Search)
変数間の依存関係をグラフ構造にマッピングし,独立性テストとスコアリングを使用して条件付き独立性を評価.DAGを見つけるための貪欲なアプローチを採用.
5.LiNGAM (Linear Non-Gaussian Acyclic Model)
線形因果モデル.独立成分分析(ICA)を使用して因果関係を推定.線形であること,非巡回であること,外生変数*4は非ガウス性*5を持つことを仮定して因果の方向性を見つける.
6.SAM (Structural Agnostic Modelling)
GANを用いて因果探索を行う.データ内の変数間の関係をモデル化する際に,事前の構造的仮定を設けない.
本記事ではPCアルゴリズム,GES,LiNGAMを利用して因果探索を行うプログラムを紹介します.
cdtを利用した因果探索
この節では実際にcdtを使って因果探索を行っていきます
インポート
必要なライブラリやモジュールをインポートします. 今回はPCアルゴリズム,GES,LiNGAMも用いるため,3つのモデルをインポートします.
import cdt from cdt.data import load_dataset from cdt.causality.graph import PC, GES, LiNGAM from cdt.metrics import precision_recall, SID, SHD import networkx as nx import matplotlib.pyplot as plt
データセット読みこみ
データセットを読み込みます 今回はSachsというデータセットを用いることとします
# データセットの読み込み
data, true_graph = load_dataset('sachs')
Sachsは細胞内のタンパク質とリン脂質の相互作用を示す生物学分野のデータセットで,因果探索のアルゴリズムの性能を評価するためのベンチマークとして広く使われています. このデータはダミーデータではなく生物学的実験に基づいた実データであるため,実際の生物学的プロセスをモデル化するアルゴリズムの有効性を評価するには適していますが,別分野での因果探索における性能については保証ができないため注意が必要です.
アルゴリズムの選択と探索
次に利用したい因果探索アルゴリズムを選び,探索を行なってみましょう
# 因果探索アルゴリズムの選択 pc = PC() # 因果関係の探索 output_pc = pc.predict(data)
この2行だけで因果探索は完了です とても簡単ですね
グラフの描画
因果探索が完了したので,結果をグラフ化して見てみましょう
# グラフの描画関数
def plot_graph(graph, title):
plt.figure(figsize=(8, 6))
nx.draw(graph, with_labels=True, node_color='lightblue', font_weight='bold', node_size=700, font_size=10)
plt.title(title)
plt.show()
# 各アルゴリズムのグラフ描画
plot_graph(output_pc, "PC Algorithm Causal Graph")
上記のプログラムを実行すると下記のようなグラフが描画できます

うまくグラフが描画できていますね
性能評価
次に先ほど探索した結果の性能評価を行います.
cdt.metrics モジュールを利用すれば,下記の3つの指標を簡単に算出することができます.
- Area under the precision recall curve(AUC)
- Structural Hamming Distance (SHD: 構造的ハミング距離)
- Structural Intervention Distance (SID:構造的介入距離)
# 性能評価関数
def evaluate_performance(predicted_graph, true_graph):
scores = [metric(true_graph, predicted_graph) for metric in (precision_recall, SID, SHD)]
return scores
# PCアルゴリズムの性能評価
scores_pc = evaluate_performance(output_pc, true_graph)
print("PC Algorithm Performance:")
print(scores_pc)
このコードを実行すると下記のような出力が得られます.
PC Algorithm Performance: [(0.2967745638200183, [(0.1487603305785124, 1.0), (0.20833333333333334, 0.2777777777777778), (1.0, 0.0)]), array(82.), 32]
GES, LINGAMでの因果探索
PCアルゴリズムでの因果探索ができたので,他のアルゴリズムでも因果探索を実施してみます.
# 因果探索アルゴリズムの選択
ges = GES()
lingam = LiNGAM()
output_ges = ges.predict(data)
output_lingam = lingam.predict(data)
plot_graph(output_ges, "GES Algorithm Causal Graph")
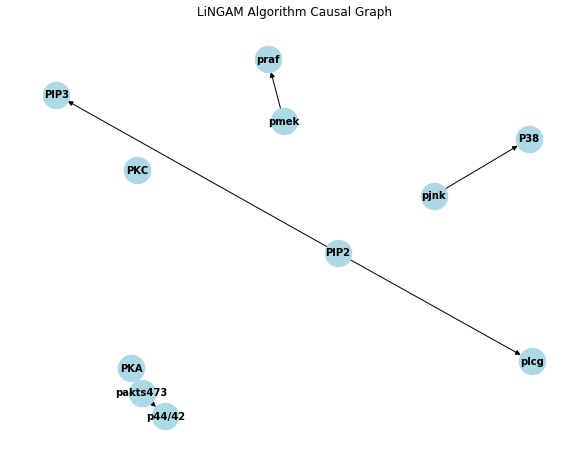
plot_graph(output_lingam, "LiNGAM Algorithm Causal Graph")
scores_ges = evaluate_performance(output_ges, true_graph)
print("\nGES Algorithm Performance:")
print(scores_ges)
scores_lingam = evaluate_performance(output_lingam, true_graph)
print("\nLiNGAM Algorithm Performance:")
print(scores_lingam)

GES Algorithm Performance: [(0.3212943387361992, [(0.1487603305785124, 1.0), (0.16279069767441862, 0.3888888888888889), (1.0, 0.0)]), array(76.), 47] LiNGAM Algorithm Performance: [(0.28787496173859806, [(0.1487603305785124, 1.0), (0.3333333333333333, 0.1111111111111111), (0.4, 0.1111111111111111), (0.25, 0.05555555555555555), (0.3333333333333333, 0.05555555555555555), (0.5, 0.05555555555555555), (1.0, 0.05555555555555555), (1.0, 0.0)]), array(80.), 20]
どのアルゴリズムを利用するかで,グラフも結果も大きく異なることがわかります.
3つの精度を比較すると下記のようになります
PC Algorithm Performance: [(0.2967745638200183, [(0.1487603305785124, 1.0), (0.20833333333333334, 0.2777777777777778), (1.0, 0.0)]), array(82.), 32] GES Algorithm Performance: [(0.3212943387361992, [(0.1487603305785124, 1.0), (0.16279069767441862, 0.3888888888888889), (1.0, 0.0)]), array(76.), 47] LiNGAM Algorithm Performance: [(0.28787496173859806, [(0.1487603305785124, 1.0), (0.3333333333333333, 0.1111111111111111), (0.4, 0.1111111111111111), (0.25, 0.05555555555555555), (0.3333333333333333, 0.05555555555555555), (0.5, 0.05555555555555555), (1.0, 0.05555555555555555), (1.0, 0.0)]), array(80.), 20]
この出力はやや読みにくいので解説します.
それぞれのアルゴリズムのパフォーマンスは,複数のメトリクスを用いて評価されています.
ここでの主要なメトリクスは,AUC,構造的ハミング距離(SHD),構造的介入距離(SID)で,下記のような順番に並んでいます.
AUC:
- 最初の数値(例:PCアルゴリズムの0.2967745638200183)はPR曲線のAUCです
- リスト内のペア(例:(0.1487603305785124, 1.0))はスコア計算に使用された適合率と再現率を示しています.最初の数値が適合率で,二番目の数値が再現率です.これらの値は,アルゴリズムがどれだけ正確に因果関係を識別し,また実際に存在する関係をどれだけ捉えたかを示しています
構造的ハミング距離(SHD):
- PCアルゴリズムのarray(82.) のような値は構造的ハミング距離を表しています
- これは,アルゴリズムが生成したグラフと真のグラフの間のエッジの違いの数を示しており,数値が小さいほど性能が良いことを意味します
構造的介入距離(SID):
- 最後の数値(例: PCアルゴリズムの32)は構造的介入距離です
- これは,アルゴリズムが生成した因果グラフと真のグラフの間の構造的な差異を評価するためのメトリクスで,こちらも数値が小さいほどより正確なグラフを生成していることを意味します
上記を踏まえると,今回の結果ではGESの結果が一番精度が良さそうです.
コード集約
先ほどまでのコードを集約すると下記のようになります.
import cdt
from cdt.data import load_dataset
from cdt.causality.graph import PC, GES, LiNGAM
from cdt.metrics import precision_recall, SID, SHD
import networkx as nx
import matplotlib.pyplot as plt
# データセットの読み込み
data, true_graph = load_dataset('sachs')
# 因果探索アルゴリズムの選択
pc = PC()
ges = GES()
lingam = LiNGAM()
# 因果関係の探索
output_pc = pc.predict(data)
output_ges = ges.predict(data)
output_lingam = lingam.predict(data)
# グラフの描画関数
def plot_graph(graph, title):
plt.figure(figsize=(8, 6))
nx.draw(graph, with_labels=True, node_color='lightblue', font_weight='bold', node_size=700, font_size=10)
plt.title(title)
plt.show()
# 各アルゴリズムのグラフ描画
plot_graph(output_pc, "PC Algorithm Causal Graph")
plot_graph(output_ges, "GES Algorithm Causal Graph")
plot_graph(output_lingam, "LiNGAM Algorithm Causal Graph")
# 性能評価関数
def evaluate_performance(predicted_graph, true_graph):
scores = [metric(true_graph, predicted_graph) for metric in (precision_recall, SID, SHD)]
return scores
# 各アルゴリズムの性能評価
scores_pc = evaluate_performance(output_pc, true_graph)
print("PC Algorithm Performance:")
print(scores_pc)
scores_ges = evaluate_performance(output_ges, true_graph)
print("\nGES Algorithm Performance:")
print(scores_ges)
scores_lingam = evaluate_performance(output_lingam, true_graph)
print("\nLiNGAM Algorithm Performance:")
print(scores_lingam)
必要なコードはこれだけです.とっても簡単ですね.
cbtで扱えないモデルについて
簡単に因果探索が試せるcdtですが,いくつか扱えないモデルも存在します.
cdtにないモデルを扱いたい場合は,cbtを自分でカスタマイズするか,他のライブラリを利用するか,著者が展開しているgit等を利用するかなどを行う必要があります.
下記にいくつかの例をご紹介します.
- LiNGAM派生モデル
- Direct LiNGAMなど,LiNGAMの派生系はまだ入っていません.
- NO TEARS
- こちらも有名なモデルですがcdtにはまだ入っていません
- 代わりにCausalNexというライブラリを使うと簡単に扱うことが可能です
最後に
今回はCausal descovery toolbox(cdt)を使って簡単に因果探索を試す方法をお伝えいたしました.
因果探索に限らずとは思いますが,様々なモデルを試したいとき個別に環境を用意するのはそれなりに大変ですし,ライブラリの依存関係につまづいたり,競合してしまったりするので,1つの環境で実施するのはさらに大変です.(筆者は環境構築が苦手なのでいつもとても苦労します)
cdtはいくつか扱えないモデルもあるものの,個別の環境構築をすることなく有名なモデルをとても簡単に試すことができるのでみなさんもぜひ試してみてください.
