この記事は、NTTドコモ R&D Advent Calendar 2022 3日目の記事です。
0. はじめに
こんにちは。 NTTドコモ無線アクセス開発部の橋本です。
5G時代を迎え、無線ネットワークはさらに複雑化が進みます。
これにより、人手による装置パラメータの最適化や保守対応が難しくなることが示唆されています。
そこで、ドコモをはじめとする多くの通信事業者が、AI/MLによる無線ネットワークの高度化を検討しています。
今回、そんな「無線ネットワークに対するAI適用ってどんな感じ?」を体験するためのシミュレーションを実装しました。
AI×無線通信分野の取り組みイメージが伝わりましたら幸いです。
1. 本記事はこんな方向け
- 無線ネットワークに対するAI適用がどのようなものか知りたい方
- 強化学習によるAI×無線ネットワーク最適化のシミュレーションをしてみたい方
2. 扱う題材 - チルト角の最適化とは?
無線ネットワークには様々な要素がありますが、今回は ”チルト角” の最適化を題材とします。
チルト角とは、無線基地局※がビームを放出している角度のことを言います。
(※無線基地局とは、無線通信を行うための装置のことです。スマートフォンなどの移動局は、基地局から発せられる電波を受信して通信を行います。)

チルト角が変化すると電波が届く範囲が変わるので、基地局配下のユーザが正しく通信できるように、適切な角度にしなければなりません。
3. 前提
簡易的に、下記の図のような3つのセル※で構成された10km四方のエリアをシミュレーション環境として設定します。
※セル=電波が繋がる1つの基地局から構成されたエリアのことを指します。

シミュレーションでは、1km毎の格子地点におけるユーザの受信電力を計算します。
前提として、3つのセル性能は全て同じであり、下記の通りであるとします。
| パラメータ | 値 |
|---|---|
| 周波数 | 500MHz |
| 送信電力 | 10dBm |
| アンテナ高(基地局側) | 30m |
| アンテナ高(受信側) | 1m |
| アンテナ指向性 | 無指向性 (360°に向けてビーム放出する) |
また、簡単のため圏外閾値の判定は考慮しません。
4. シミュレーション環境の準備
まずは、実験用のシミュレーション環境を用意します。
シミュレーション環境は、pythonのクラスを定義することによって作成します。
4.1 ライブラリ
以下のpythonライブラリを用います。
import math import seaborn as sns import pandas as pd import numpy as np import matplotlib.pyplot as plt
3-2. クラス定義
シミュレーション環境を定義するpythonのクラスを以下のように定義します。
初期値として基地局の位置x1_num, y1_numとチルト角tilt_baseを入力することで、現在の環境におけるシミュレーションエリアの電力マップpower_locを生成します。
なお、電力マップは二次元配列として管理し、各要素は1km格子地点における電力の値を指すものとします。
例えば、以下のような電力マップが生成された場合、
# [[-118.14091671101016, -114.72727547900973], # [-118.44091517114933, -115.1909920136982,]]
- x軸方向0km、y軸方向0km地点における受信電力は-118.14(dB)
- x軸方向0km、y軸方向1km地点における受信電力は-114.72(dB)
- …
と読み替えます。
class Cell: def __init__(self, tilt_base=None, x1_num=None, y1_num=None, power_loc=None): if power_loc is None: self.power_loc = [[0 for j in range(10)] for i in range(10)] # エリア全体の電力を初期化 self.tilt_base = tilt_base # チルト角 self.x1 = x1_num # 基地局の位置(x軸) self.y1 = y1_num # 基地局の位置(y軸) Cell.calc_power_loc(self) # エリア全体の電力マップ else: self.power_loc = power_loc
1km毎の地点に移動局が配置されていると仮定し、エリア全体の電力マップを作成する関数です。
基地局と移動局間の距離とアンテナゲインの情報をcalc_receive_power関数に引き渡し算出します。
def calc_power_loc(self): # 電力マップ作成関数 for i in range(0,10): for j in range(0,10): x2=i # 移動局の位置(x軸) y2=j # 移動局の位置(y軸) dist = Cell.calc_dist(self.x1,self.y1,x2,y2) # 基地局と移動局間の距離(km) tilt_current=Cell.calc_tilt_current(dist*1000) # 基地局と移動局間の角度(°) ant_gain = Cell.calc_ant_gain(self.tilt_base, tilt_current) # 移動局位置のアンテナゲイン(dB) self.power_loc[i][j]=Cell.calc_receive_power(dist, ant_gain)
基地局と移動局間の距離を計算する関数です。
def calc_dist(x1,y1,x2,y2): # 距離計算関数(m) if (x1==x2)&(y1==y2): return 0 elif x1==x2: return abs(y1-y2) elif y1==y2: return abs(x1-x2) else: return math.sqrt(pow((x1-x2),2)+pow((y1-y2),2))
三角関数を用いて、移動局から見た基地局の仰角を求める関数です。
def calc_tilt_current(dist, height_t=30, height_r=5): # 基地局と移動局間の仰角を求める if dist==0: return 90 else: return math.degrees(math.atan((height_t-height_r)/dist))
チルト角、移動局から見た基地局の仰角などの情報からアンテナゲイン※を算出する関数です。
※アンテナゲインとは、移動局のアンテナが受信した電力のことです。アンテナのビーム照射位置から近いほど大きく、遠ざかる程小さくなります。
def calc_ant_gain(tilt_base, tilt_current, tilt_m3db=6.5, am=18):# アンテナゲイン(dB)を算出する関数 ant_gain = am tmp_gain = 12 * pow(((tilt_current - tilt_base) / tilt_m3db),2) if tmp_gain < ant_gain: ant_gain = tmp_gain return -ant_gain
パスロス※やアンテナゲインから、移動局の受信電力を計算する関数です。
※パスロスとは、電波の減衰量のことです。今回は、奥村・秦モデルの開放地モデルによって計算します。
本来、建物の反射波や給電線損失など様々な要因によって電波が減衰しますが、今回は簡易のため考慮しません。
def calc_receive_power(dist, ant_gain, freq=500, power_t=10, height_t=30, height_r=5): A = 69.55 + 26.16 * math.log10(freq) - 13.82 * math.log10(height_t) B = 44.9 - 6.55 * math.log10(height_t) alpha = (1.1 * math.log10(freq) - 0.7) * height_r - (1.56 * math.log10(freq)-0.8) C = -4.78 * (math.log10(freq) * math.log10(freq)) + 18.33 * math.log10(freq)-40.94 if dist==0: power_r = 0 else: loss = A + B * math.log10(dist) - alpha + C power_r = power_t - loss + ant_gain return power_r #受信電力(dB)
電力マップをプロットする関数です。
def plot_loc(self):# plot df_power_loc=pd.DataFrame(self.power_loc) df_power_loc=df_power_loc.replace(0, np.nan) #基地局直下をnanで埋める sns.heatmap(df_power_loc, annot=True, fmt="1.1f", annot_kws={"size":8}, vmin=-130, vmax=-85) plt.figure()
それでは、作成したCellクラスを用いて、以下のように実行してみましょう。
# cell1 cell1 = Cell(tilt_base=10,x1_num=0,y1_num=5) cell1.calc_power_loc() cell1.plot_loc()

セルが1つの場合の電力マップを表示できました!
次に、3セルで構成されたエリアの電力マップを作成してみましょう。
複数のセルで構成されるエリアの場合、各地点で最も電力値の高い値を採用します。
# cell1 cell1 = Cell(tilt_base=10,x1_num=0,y1_num=5) # cell2 cell2 = Cell(tilt_base=10,x1_num=7,y1_num=0) # cell3 cell3 = Cell(tilt_base=10,x1_num=8,y1_num=8) # 各メッシュにおける最大電力値を取得する sum_power_loc = np.maximum(cell1.power_loc, cell2.power_loc) sum_power_loc = np.maximum(sum_power_loc,cell3.power_loc) cell_sum=Cell(power_loc=sum_power_loc) cell_sum.plot_loc()

3セルで構成されたエリアの電力マップを表示できました!
これで、各セルのチルト角を変更した時に、どのようにエリアが変化するかをシミュレーションできる環境が整いました。
4. 実装
先ほど作成したシミュレーション環境を用いて、チルト角の最適化を行います。
用いるアルゴリズムは、強化学習(DQN)です。
4.1 DQNとは
DQNとは、Deep Q Networkの略称で、同じく強化学習の一種であるQ学習においてQ関数(状態行動価値関数)をニューラルネットワークによって表した手法のことを言います。
4.2 環境設計
強化学習の要素である環境を、OPEN AI Gymを用いて作成します。
以下の通りTiltクラスとして定義します。
class Tilt(gym.Env): def __init__(self): super(Tilt, self).__init__() self.agent_pos = np.array([10,10,10]) # 初期チルト角の指定 # 行動空間と状態空間の定義 self.action_space = gym.spaces.Discrete(6) self.observation_space = gym.spaces.Box( low=0, high=4, shape=(3,6),# 状態空間と行動空間の次元 dtype=np.float32) self.reset() def reset(self): # 環境のリセット self.agent_pos = np.array([10,10,10])# 初期位置の指定 return self.agent_pos def step(self, action):# 環境の1ステップ実行 # 報酬の計算(前) cell1 = Cell(tilt_base=self.agent_pos[0],x1_num=0,y1_num=5) # セル1の電力マップ作成 cell2 = Cell(tilt_base=self.agent_pos[1],x1_num=7,y1_num=0) # セル2の電力マップ作成 cell3 = Cell(tilt_base=self.agent_pos[2],x1_num=8,y1_num=8) # セル3の電力マップ作成 sum_power_loc = np.maximum(np.maximum(cell1.power_loc, cell2.power_loc),cell3.power_loc) # エリア全体の電力マップ作製 cell_sum=Cell(power_loc=sum_power_loc) ave_old = np.average(cell_sum.power_loc)# エリア全体の受信電力平均値(チルト変更前) # チルト角の変更 if action==0: # Cell 1のチルト角を-1°変更 self.agent_pos = np.array([self.agent_pos[0]-1,self.agent_pos[1],self.agent_pos[2]]) elif action==1: # Cell 1のチルト角を+1°変更 self.agent_pos = np.array([self.agent_pos[0]+1,self.agent_pos[1],self.agent_pos[2]]) elif action==2: # Cell 2のチルト角を-1°変更 self.agent_pos = np.array([self.agent_pos[0],self.agent_pos[1]-1,self.agent_pos[2]]) elif action==3: # Cell 2のチルト角を+1°変更 self.agent_pos = np.array([self.agent_pos[0],self.agent_pos[1]+1,self.agent_pos[2]]) elif action==4: # Cell 3のチルト角を-1°変更 self.agent_pos = np.array([self.agent_pos[0],self.agent_pos[1],self.agent_pos[2]-1]) elif action==5: # Cell 3のチルト角を+1°変更 self.agent_pos = np.array([self.agent_pos[0],self.agent_pos[1],self.agent_pos[2]+1]) self.agent_pos = np.clip(self.agent_pos, 8, 12) # チルト角の動作できる範囲を8°~12°にクリップ done = self.agent_pos == np.array([5,5,5]) # エピソード完了の計算 # 報酬の計算 cell1 = Cell(tilt_base=self.agent_pos[0],x1_num=0,y1_num=5) # セル1の電力マップ作成 cell2 = Cell(tilt_base=self.agent_pos[1],x1_num=7,y1_num=0) # セル2の電力マップ作成 cell3 = Cell(tilt_base=self.agent_pos[2],x1_num=8,y1_num=8) # セル3の電力マップ作成 sum_power_loc = np.maximum(np.maximum(cell1.power_loc, cell2.power_loc),cell3.power_loc) # エリア全体の電力マップ作製 cell_sum=Cell(power_loc=sum_power_loc) ave_new = np.average(cell_sum.power_loc)# エリア全体の受信電力平均値(チルト変更後) if ave_old < ave_new: # 受信電力の平均値が上昇した場合 reward=1 else: # 受信電力の平均値が減少もしくは同値である場合 reward=-1 return np.array(self.agent_pos).astype(np.float32), reward, done, {} # 環境の描画 def render(self, mode='console', close=False): pass
全てのセルにおいて初期のチルト角は10°としています。
self.agent_pos = np.array([10,10,10]) # 初期チルト角の指定
4.2.1 行動
一回の行動につき、一つのセルに対してチルト角を+1°もしくは-1°変更させることを想定します。
なお、簡易のため、チルト角の制御範囲を8°~12°に制限します。
エージェントは、以下の全6つの行動の中からランダムに1つの行動を選択します。
- セル1のチルト角を1°下げる
- セル1のチルト角を1°上げる
- セル2のチルト角を1°下げる
- セル2のチルト角を1°上げる
- セル3のチルト角を1°下げる
- セル3のチルト角を1°上げる
4.2.2 報酬
エリア全体の受信電力が上昇する方向に学習が進むよう、以下の通り報酬を設計します。
- 前回の状態と比べて、現在のエリアにおける平均受信電力が上昇した場合、+1を報酬として与える
- 前回の状態と比べて、現在のエリアにおける平均受信電力が減少もしくは同値の場合、-1を報酬として与える
if ave_old < ave_new: # 受信電力の平均値が上昇した場合 reward=1 else: # 受信電力の平均値が減少もしくは同値である場合 reward=-1
なお、平均受信電力(dB)は、全エリアにおける1km単位の受信電力の平均値として算出します。
np.average(cell_sum.power_loc)
4.3 全体設計
DQNを用いた学習を設計していきますエリア内の受信電力が最大となるチルト角を学習します。
こちらの記事を大いに利用させていただいたため、詳細説明は割愛いたします。
# トランザクション処理用tuple変数の用意 from collections import namedtuple Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward')) # 定数の設定 GAMMA = 0.5 # 時間割引率 MAX_STEPS = 8 # 1試行のstep数 NUM_EPISODES = 3000 # 最大試行回数 # 経験を保存するメモリクラスの定義 class ReplayMemory: def __init__(self, CAPACITY): self.capacity = CAPACITY # メモリの最大長さ self.memory = [] # 経験を保存する変数 self.index = 0 # 保存するindexを示す変数 def push(self, state, action, state_next, reward): if len(self.memory) < self.capacity: self.memory.append(None) # メモリが満タンでないときは足す # namedtupleのTransitionを使用し、値とフィールド名をペアにして保存 self.memory[self.index] = Transition(state, action, state_next, reward) self.index = (self.index + 1) % self.capacity # 保存するindexを1つずらす def sample(self, batch_size): # batch_size分ランダムに保存内容を取得 return random.sample(self.memory, batch_size) def __len__(self): return len(self.memory) # Q関数をディープラーニングのネットワークをクラスとして定義 import random import torch from torch import nn from torch import optim import torch.nn.functional as F from torch.autograd import Variable BATCH_SIZE = 32 CAPACITY = 10000 class Brain: def __init__(self, num_states, num_actions): self.num_states = num_states # CartPoleは状態数4を取得 self.num_actions = num_actions # CartPoleの行動(右に左に押す)の2を取得 # 経験を記憶するメモリオブジェクトを生成 self.memory = ReplayMemory(CAPACITY) # ニューラルネットワークを構築 self.model = nn.Sequential() self.model.add_module('fc1', nn.Linear(self.num_states, 32)) self.model.add_module('relu1', nn.ReLU()) self.model.add_module('fc2', nn.Linear(32, 32)) self.model.add_module('relu2', nn.ReLU()) self.model.add_module('fc3', nn.Linear(32, self.num_actions)) print(self.model) # ネットワークの形を出力 # 最適化手法の設定 self.optimizer = optim.Adam(self.model.parameters(), lr=0.0001) def replay(self): # リプレイ(経験が句集) if len(self.memory) < BATCH_SIZE: # メモリサイズがミニバッチより小さい間は何もしない return # メモリからミニバッチ分のデータを取り出す transitions = self.memory.sample(BATCH_SIZE) # ミニバッチの作成----------------- batch = Transition(*zip(*transitions)) non_final_mask = torch.BoolTensor(tuple(map(lambda s: s is not None,batch.next_state))) state_batch = Variable(torch.cat(batch.state)) action_batch = Variable(torch.cat(batch.action)) reward_batch = Variable(torch.cat(batch.reward)) non_final_next_states = Variable(torch.cat([s for s in batch.next_state if s is not None])) # ミニバッチの作成終了------------------ # ネットワークを推論モードに切り替える self.model.eval() state_action_values = self.model(state_batch).gather(1, action_batch) # Q(s_t, a_t)を求める next_state_values = Variable(torch.zeros( BATCH_SIZE).type(torch.FloatTensor)) # max{Q(s_t+1, a)}値を求める。次の状態がない場合は0 next_state_values[non_final_mask] = self.model(non_final_next_states).data.max(1)[0] # 次の状態がある場合の値を求める expected_state_action_values = reward_batch + GAMMA * next_state_values# 教師となるQ(s_t, a_t)値を求める # ネットワークを訓練モードに切り替える self.model.train() # 損失関数を計算 expected_state_action_values = expected_state_action_values.unsqueeze(1) loss = F.smooth_l1_loss(state_action_values, expected_state_action_values) # ネットワークを更新 self.optimizer.zero_grad() # 勾配をリセット loss.backward() # バックプロパゲーションを計算 self.optimizer.step() # 結合パラメータを更新 return loss def decide_action(self, state, episode): # ε-greedy法で徐々に最適行動のみを採用する epsilon = 1 episode_down=1 if (episode>=episode_down): epsilon = 0.999 - (0.001*(episode-episode_down)) if epsilon <= 0: epsilon = 0.001 if epsilon <= np.random.uniform(0, 1): self.model.eval() # ネットワークを推論モードに切り替える action = self.model(Variable(state)).data.max(1)[1].view(1, 1) else: action = torch.LongTensor([[random.randrange(self.num_actions)]]) # 行動をランダムに返す return action, epsilon class Agent: def __init__(self, num_states, num_actions): # 状態と行動の数の設定 self.num_states = num_states self.num_actions = num_actions self.brain = Brain(num_states, num_actions) def update_q_function(self): # Q関数の更新 loss=self.brain.replay() return loss def get_action(self, state, step): # 行動の決定 action, epsilon = self.brain.decide_action(state, step) return action, epsilon def memorize(self, state, action, state_next, reward): self.brain.memory.push(state, action, state_next, reward) def get_model(self): return self.brain.model class Environment: def __init__(self): self.env = Tilt() self.num_states = self.env.observation_space.shape[0] # 状態と行動の数を設定 self.num_actions = self.env.action_space.n # 行動を取得 self.agent = Agent(self.num_states, self.num_actions) self.total_step = np.zeros(MAX_STEPS) def run(self): """メインの実行""" total_reward = [] # eps報酬格納用 total_state = [] # eps状態格納用 total_loss = [] # loss格納用 for episode in range(NUM_EPISODES): # 試行数分繰り返す observation = self.env.reset() # 環境の初期化 state = observation # 観測をそのまま状態sとして使用 state = torch.from_numpy(state).type(torch.FloatTensor) # numpy変数をPyTorchのテンソルに変換 total_reward_epi=0 # 各エピソードの累積報酬 total_loss_epi=0 # 各エピソードの累積報酬 total_action = [] # 累積行動格納用 tota_state = [] # 累積状態格納用 eps_reward = [] # 今、FloatTensorof size 4になっているので、size 1x4に変換 state = torch.unsqueeze(state, 0) for step in range(MAX_STEPS): # 1エピソードのループ action, epsilon = self.agent.get_action(state, episode) # 行動を求める observation_next, reward, done, _ = self.env.step(action[0, 0].item()) now_reward=reward total_reward_epi+=reward reward = torch.FloatTensor([reward]) state_next = observation_next # 観測をそのまま状態とする state_next = torch.from_numpy(state_next).type(torch.FloatTensor) # numpyとPyTorchのテンソルに state_next = torch.unsqueeze(state_next, 0) # size 1x4に変換 self.agent.memorize(state, action, state_next, reward)# メモリに経験を追加 loss=self.agent.update_q_function()# Experience ReplayでQ関数を更新する if loss is not None: total_loss_epi+=loss.item() # 観測の更新 state = state_next # 累積行動と状態をappend if episode==NUM_EPISODES-1: total_action.append(action[0, 0].item()) total_state.append(observation_next.tolist()) eps_reward.append(reward.item()) print('%d Episode: Finished after %d steps:reward = %.1lf : epsilon = %.3lf : loss = %.3lf' % ( episode, step + 1, total_reward_epi, epsilon, total_loss_epi)) # 累積報酬をappend total_reward.append(total_reward_epi) total_loss.append(total_loss_epi) return self.agent.get_model(),total_reward,total_state,eps_reward,total_action,total_loss
実行結果
以下を実行することで実行結果が得られます。
env = Environment() agents,total_reward,total_state,eps_reward,total_action,total_loss=env.run()
# 実行結果 Sequential( (fc1): Linear(in_features=3, out_features=32, bias=True) (relu1): ReLU() (fc2): Linear(in_features=32, out_features=32, bias=True) (relu2): ReLU() (fc3): Linear(in_features=32, out_features=6, bias=True) ) 0 Episode: Finished after 8 steps:reward = -8.0 : epsilon = 1.000 : loss = 0.000 1 Episode: Finished after 8 steps:reward = 0.0 : epsilon = 0.999 : loss = 0.000 2 Episode: Finished after 8 steps:reward = -6.0 : epsilon = 0.998 : loss = 0.000 3 Episode: Finished after 8 steps:reward = 2.0 : epsilon = 0.997 : loss = 0.349 4 Episode: Finished after 8 steps:reward = 0.0 : epsilon = 0.996 : loss = 2.931 5 Episode: Finished after 8 steps:reward = -6.0 : epsilon = 0.995 : loss = 2.647 ...
最適化過程をグラフに表すと、以下のようになりました。
plt.figure(figsize=(15,7)) tmp = np.array(total_reward, dtype="float32") plt.plot(tmp, color="cyan") plt.show()

ステップが進むにつれて、高い報酬を得られるように動作できているのが確認できますね!
最後に、最終的に出力されたチルト角を確認し、シミュレーション環境で表示してみましょう。
total_state
# 出力結果 [[10.0, 9.0, 10.0], [10.0, 9.0, 9.0], [9.0, 9.0, 9.0], [9.0, 8.0, 9.0], [9.0, 8.0, 8.0], [8.0, 8.0, 8.0], [8.0, 8.0, 8.0], [8.0, 8.0, 8.0]] # 最終的なチルト角
シミュレーション環境上で、全セルのチルト角が8°である場合をプロットすると…
cell1 = Cell(tilt_base=8,x1_num=0,y1_num=5) cell2 = Cell(tilt_base=8,x1_num=7,y1_num=0) cell3 = Cell(tilt_base=8,x1_num=8,y1_num=8) sum_power_loc = np.maximum(np.maximum(cell1.power_loc, cell2.power_loc),cell3.power_loc) cell_sum=Cell(power_loc=sum_power_loc) cell_sum.plot_loc() print(np.average(cell_sum.power_loc)) # エリア全体の受信電力平均値(チルト変更後)
-102.74266185631082

このようになりました。
最適化前の、全セルのチルト角が10°である場合と比較すると…
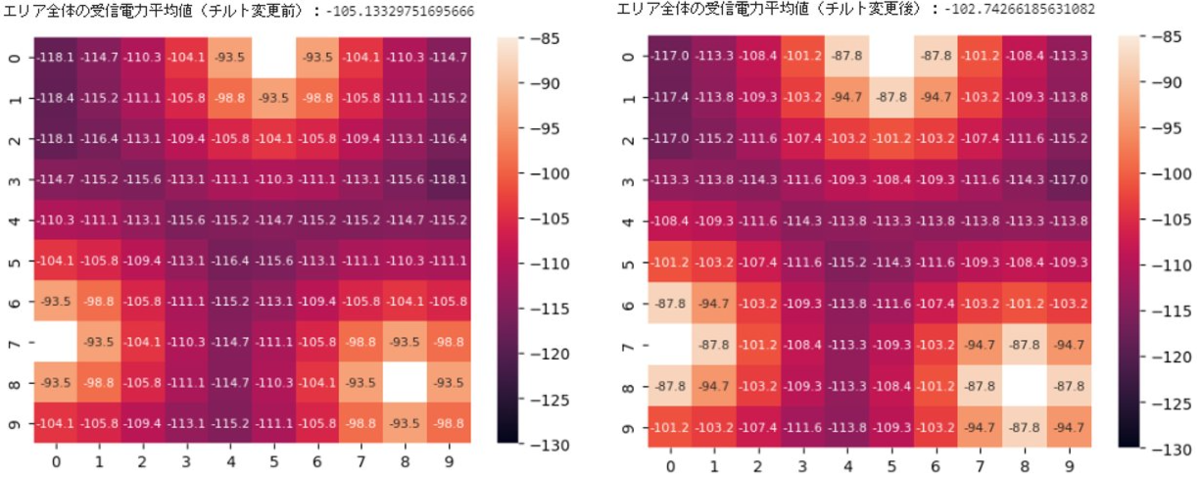
エリア全体の受信電力の平均値の引き上げに(微量ですが)成功しました!
さいごに
今回、強化学習によるチルト角の最適化を実装しました。
このように、何ステップも学習を繰り返す最適化は、現在の基地局やそれを取り巻く環境では実現が難しい部分もあります。
また、今回のような簡易なケースでは、シミュレーション環境下で全探索した方が良いとも考えられます。
しかし、より複雑な最適化が必要となった際は、無線ネットワークの分野にもAIやMLの力が必要になることでしょう。
ドコモでは、より高度な無線ネットワークの最適化を実施できるように、環境整備を進めています。
今回の投稿で、無線ネットワーク×AIの取り組みについて、少しでもご興味を持っていただけたら幸いです!
参考
今回の投稿では以下の記事を参考にしました。
