機械学習で総合格闘技の勝敗予想してみた

はじめに

この記事はNTTドコモアドベントカレンダーの21日目の記事です。

こんにちは、NTTドコモサービスイノベーション部の川嶋です。
普段の業務では画像認識技術を用いたサービス開発に取り組んでおり、スポーツ解析、自動運転系の案件に携わっています。

最近、日本で総合格闘技のブームが再び到来しています。
格闘技では、試合が決まってから試合当日までファンの間で勝敗予想をするのも楽しみのひとつですよね。
ということで、今回は統計データと機械学習を使って総合格闘技の勝敗予想をしてみたいと思います！

データセット

kaggleで提供されているUFC※のデータセット(data.csv)を使います。
このデータセットには、1993年から2021年までにUFCで行われた試合における、 両選手の現在の試合を除いた全ての試合に準拠した統計情報と、現在の試合で対戦相手に与えたダメージなどの情報が含まれています。
各カラムの詳細が気になる方はこちらをご覧ください。

※UFC（Ultimate Fighting Championship）とはアメリカの実力・人気ともに世界最大級の総合格闘技団体のことです。 ちなみに、UFCには日本からは平良達郎選手、木下憂朔選手などの数名の選手が参戦しています。

実装方針

UFCデータセットにおけるWinnerカラムを目的変数、それ以外のカラムの情報を説明変数とした分類モデルを作成します。
Winnerカラムには試合の勝敗（Blue（青コーナーの選手）, Red（赤コーナー）, Draw）が格納されているので、3クラスに分類する必要があります。
まずはじめに、データセットの行数・列数や各列のデータ型、欠損値ではない要素の数などの要約情報を出力するとともに、目的変数であるWinnerカラムの分布をヒストグラムで可視化してみます。
また、Winnerカラムに格納されているカテゴリー変数を数値に変換しておきます。

import pandas as pd

df = pd.read_csv("./archive/data.csv")
df.info()

#目的変数：カテゴリー変数を数値に変換　Rが勝者なら1、drawなら2
y = df['Winner'].map({'Blue':0, 'Red':1, 'Draw':2})

#ヒストグラム表示
plt.hist(y, range = (0, 2), bins = 3)
plt.xticks([0, 1, 2])

データフレームの要約情報は下記の通りです。
約6,000試合分のデータがあり、カラムは88個あります。
欠損値も多く含まれているので、うまく補完して機械学習する必要がありそうです。

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 6012 entries, 0 to 6011
Data columns (total 88 columns):
 #   Column                        Non-Null Count  Dtype  
---  ------                        --------------  -----  
 0   title_bout                    6012 non-null   bool   
 1   weight_class                  6012 non-null   object 
 2   B_avg_KD                      4585 non-null   float64
 3   B_avg_SIG_STR_pct             4585 non-null   float64
 4   B_avg_TD_pct                  4585 non-null   float64
 5   B_avg_SUB_ATT                 4585 non-null   float64
 6   B_avg_REV                     4585 non-null   float64
 7   B_avg_SIG_STR_att             4585 non-null   float64
 8   B_avg_SIG_STR_landed          4585 non-null   float64
 9   B_avg_TOTAL_STR_att           4585 non-null   float64
 10  B_avg_TOTAL_STR_landed        4585 non-null   float64
︙（省略）
 80  R_win_by_KO/TKO               6012 non-null   int64  
 81  R_win_by_Submission           6012 non-null   int64  
 82  R_win_by_TKO_Doctor_Stoppage  6012 non-null   int64  
 83  R_Stance                      5983 non-null   object 
 84  R_Height_cms                  6008 non-null   float64
 85  R_Reach_cms                   5606 non-null   float64
 86  B_age                         5840 non-null   float64
 87  R_age                         5949 non-null   float64
dtypes: bool(1), float64(56), int64(28), object(3)
memory usage: 4.0+ MB

また、Winnerカラムの分布は下記のようになりました。
赤コーナー(1)の勝利数が3979で総データ数6012の約66%を占めており、Draw判定(2)の試合はわずか100試合程度でした。
このラベルの不均衡の原因は、格闘技では通常、「赤コーナー」はランキング上位の選手、「青コーナー」にはランキング下位の選手が割り当てられることが多いためだと思われます（例えばタイトルマッチであれば、チャンピオンが赤コーナー、チャレンジャーが青コーナーになります）。

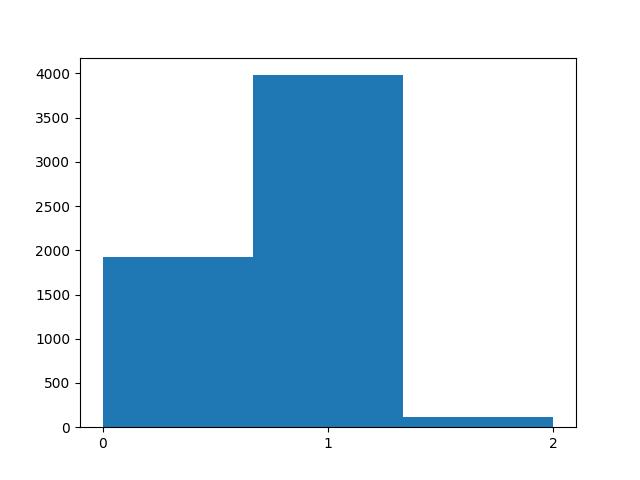
Drawを正確に判定するのはかなり難しそうですが、何も考えずに赤コーナーが勝利すると予想すれば、今回のデータでは66%の確率で正解することができます。
なので、今回は66%を超える精度で勝敗を予想できるモデルの作成を目指します！

特徴量生成

このセクションでは特徴量の選択・生成方法を説明します。
まず、下記カラムを特徴量から除外します。

• 目的変数となるWinnerカラム
• カラム名に「opp」が含まれているカラム
  • 現在の試合の対戦相手に対する統計情報のため。
• 計量体重に関するカラム（R_Weight_lbs、B_Weight_lbs）
  • 計量体重は階級ごとに全選手がほぼ同じ体重なため。元UFC世界ミドル級王者アデサニヤがライトヘビー級タイトルマッチに挑戦したとき、リミットから約2kgアンダーだったという例外もありますが…

# 除外するカラム以外を選択して読み込み
df = df [['title_bout', 'weight_class', 
          'B_avg_KD', 'B_avg_SIG_STR_pct', 'B_avg_TD_pct', 'B_avg_SUB_ATT', 'B_avg_REV', 'B_avg_SIG_STR_att', 'B_avg_SIG_STR_landed', 'B_avg_TOTAL_STR_att', 'B_avg_TOTAL_STR_landed', 'B_avg_TD_att', 'B_avg_TD_landed', 'B_avg_HEAD_att', 'B_avg_HEAD_landed', 'B_avg_BODY_att', 'B_avg_BODY_landed', 'B_avg_LEG_att', 'B_avg_LEG_landed', 'B_avg_DISTANCE_att', 'B_avg_DISTANCE_landed', 'B_avg_CLINCH_att', 'B_avg_CLINCH_landed', 'B_avg_GROUND_att', 'B_avg_GROUND_landed', 'B_avg_CTRL_time(seconds)', 'B_total_time_fought(seconds)', 'B_total_rounds_fought', 'B_total_title_bouts', 'B_current_win_streak', 'B_current_lose_streak', 'B_longest_win_streak', 'B_wins', 'B_losses', 'B_draw', 'B_win_by_Decision_Majority', 'B_win_by_Decision_Split', 'B_win_by_Decision_Unanimous', 'B_win_by_KO/TKO', 'B_win_by_Submission', 'B_win_by_TKO_Doctor_Stoppage', 'B_Stance', 'B_Height_cms', 'B_Reach_cms',
          'R_avg_KD', 'R_avg_SIG_STR_pct', 'R_avg_TD_pct', 'R_avg_SUB_ATT', 'R_avg_REV', 'R_avg_SIG_STR_att', 'R_avg_SIG_STR_landed', 'R_avg_TOTAL_STR_att', 'R_avg_TOTAL_STR_landed', 'R_avg_TD_att', 'R_avg_TD_landed', 'R_avg_HEAD_att', 'R_avg_HEAD_landed', 'R_avg_BODY_att', 'R_avg_BODY_landed', 'R_avg_LEG_att', 'R_avg_LEG_landed', 'R_avg_DISTANCE_att', 'R_avg_DISTANCE_landed', 'R_avg_CLINCH_att', 'R_avg_CLINCH_landed', 'R_avg_GROUND_att', 'R_avg_GROUND_landed', 'R_avg_CTRL_time(seconds)', 'R_total_time_fought(seconds)', 'R_total_rounds_fought', 'R_total_title_bouts', 'R_current_win_streak', 'R_current_lose_streak', 'R_longest_win_streak', 'R_wins', 'R_losses', 'R_draw', 'R_win_by_Decision_Majority', 'R_win_by_Decision_Split', 'R_win_by_Decision_Unanimous', 'R_win_by_KO/TKO', 'R_win_by_Submission', 'R_win_by_TKO_Doctor_Stoppage', 'R_Stance', 'R_Height_cms', 'R_Reach_cms', 
          'B_age', 'R_age']]
df.head(5)

上記のようにデータセットには欠損値が含まれているので、欠損値を下記の方針で補完します。

• B_age, R_age（年齢）のような身体的な特徴以外の特徴量はそれぞれのカラムの平均値で補完
• B_Stance, R_Stance（オーソドックス、サウスポーなど）のようなカテゴリー変数は最頻値で補完し、One-Hotエンコーディング
• B_Height_cms（身長）, B_Reach_cms（リーチ）のような身体的な特徴は階級ごとに分布が異なるはずなので、階級ごとの平均値で補完（※）

※本来であればキャッチウェイトの場合は例外的な処理をしなければいけないですが、キャッチウェイトの試合数は少ないこともあり、他の階級と同様に平均値で補完しました。
キャッチウェイトとは正規の階級の規定体重ではなく、事前に両選手間の合意のもとその1戦に限り定められる体重で試合が行われることです。例えばライト級の選手と、フェザー級の選手が試合をしようとするときに、ライト級とフェザー級の中間の体重で試合が行われたりします。 このことから、キャッチウェイトで実施された試合の体重はどの選手同士が試合をするかによって決まっているはずなので、平均値で補完する手法は相応しくない可能性があります。

ここで、身体的な特徴が本当に階級ごとに分布が異なるのか可視化して確かめてみます。 DataFrameからB_Height_cms, B_Reach_cmsを選択し、それぞれの分布をボックスプロットで可視化してみます。 （データの見やすさを考慮し、男性選手のフライ、バンタム、フェザー、ライト級（軽い順に4階級選択）に絞って可視化します。）

import matplotlib.pyplot as plt

weight_classes = ['Flyweight', 'Bantamweight', 'Featherweight', 'Lightweight']
height_s = [df[df['weight_class'] == cls]['B_Height_cms'] for cls in weight_classes]
reach_s = [df[df['weight_class'] == cls]['B_Reach_cms'] for cls in weight_classes]

fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
ax1.boxplot([height_s[0].dropna(), height_s[1].dropna(), height_s[2].dropna(), height_s[3].dropna()], labels=['Flyweight', 'Bantamweight', 'Featherweight', 'Lightweight'])
ax1.set_xlabel('Weight class')
ax1.set_ylabel('Height [cm]')
ax1.set_ylim(140, 220)
plt.xticks(rotation=45)

ax2 = fig.add_subplot(1, 2, 2)
ax2.boxplot([reach_s[0].dropna(), reach_s[1].dropna(), reach_s[2].dropna(), reach_s[3].dropna()], labels=['Flyweight', 'Bantamweight', 'Featherweight', 'Lightweight'])
ax2.set_xlabel('Weight class')
ax2.set_ylabel('Reach [cm]')
ax2.set_ylim(140, 220)
plt.xticks(rotation=45)

plt.tight_layout()
plt.show()

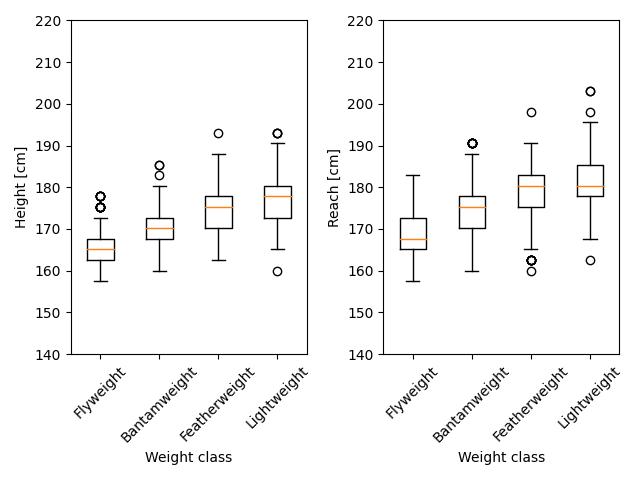
予想通り、いずれの特徴量も階級ごとに平均値も高くなる傾向にあるので、身体的な特徴は階級ごとの平均値で補完したほうがよさそうです。
それでは、次に実際に上記の方針に従って欠損値を補完していきます。

#B_age, R_age（年齢）などの身体的な特徴以外の特徴量はそれぞれのカラムの平均値で補完する。
columns = ['B_age', 'R_age',
           'B_avg_KD', 'B_avg_SIG_STR_pct', 'B_avg_TD_pct', 'B_avg_SUB_ATT', 'B_avg_REV', 'B_avg_SIG_STR_att', 'B_avg_SIG_STR_landed', 'B_avg_TOTAL_STR_att', 'B_avg_TOTAL_STR_landed', 'B_avg_TD_att', 'B_avg_TD_landed', 'B_avg_HEAD_att', 'B_avg_HEAD_landed', 'B_avg_BODY_att', 'B_avg_BODY_landed', 'B_avg_LEG_att', 'B_avg_LEG_landed', 'B_avg_DISTANCE_att', 'B_avg_DISTANCE_landed', 'B_avg_CLINCH_att', 'B_avg_CLINCH_landed', 'B_avg_GROUND_att', 'B_avg_GROUND_landed', 'B_avg_CTRL_time(seconds)', 'B_total_time_fought(seconds)',
           'R_avg_KD', 'R_avg_SIG_STR_pct', 'R_avg_TD_pct', 'R_avg_SUB_ATT', 'R_avg_REV', 'R_avg_SIG_STR_att', 'R_avg_SIG_STR_landed', 'R_avg_TOTAL_STR_att', 'R_avg_TOTAL_STR_landed', 'R_avg_TD_att', 'R_avg_TD_landed', 'R_avg_HEAD_att', 'R_avg_HEAD_landed', 'R_avg_BODY_att', 'R_avg_BODY_landed', 'R_avg_LEG_att', 'R_avg_LEG_landed', 'R_avg_DISTANCE_att', 'R_avg_DISTANCE_landed', 'R_avg_CLINCH_att', 'R_avg_CLINCH_landed', 'R_avg_GROUND_att', 'R_avg_GROUND_landed', 'R_avg_CTRL_time(seconds)', 'R_total_time_fought(seconds)'
          ]
[df[col].fillna(df[col].mean(), inplace=True) for col in columns]

#B_Stance, R_Stanceはそれぞれのカラムの最頻値で補完する。（ちなみに最頻値はオーソドックスでした）
df['B_Stance'].fillna(df['B_Stance'].mode()[0], inplace=True)
df['R_Stance'].fillna(df['R_Stance'].mode()[0], inplace=True)

#身体的な特徴は階級ごとの平均値で補完する。
columns = ['B_Height_cms', 'B_Reach_cms', 'R_Height_cms', 'R_Reach_cms']
for col in columns:
    #NaNが含まれている階級を重複なく抽出
    for cls in df[df[col].isnull()]['weight_class'][~df[df[col].isnull()]['weight_class'].duplicated()]:
        avg = df[df['weight_class'] == cls][col].mean() # NaNが含まれている階級の平均値を算出
        #無差別級の全選手のB_Reach_cmsがNaNだったため、1つ下の階級のライトヘビー級の平均値で補完
        if col == 'B_Reach_cms' and cls == 'OpenWeight':
            avg = df[df['weight_class'] == 'LightHeavyweight']['B_Reach_cms'].mean()
        df.loc[df.weight_class==cls, col] = df.loc[df.weight_class==cls, col].fillna(avg) #NaNのレコードを平均値で補完

最後に、カテゴリー変数の処理をします。

#bool値を0,1（title戦を1 ）に変換
df['title_bout'] = df.apply(lambda x: 0 if x['title_bout'] == False else 1, axis=1)
#カテゴリー値をOne-Hotエンコーディング（最初のカテゴリーが除外されたn-1個のダミー変数に変換）
df = pd.get_dummies(df, columns=['weight_class', 'R_Stance', 'B_Stance'], drop_first=True)

データ分割・前処理

本来であればホールドアウト検証・交差検証で汎用性を確認すべきですが、今回は簡易的にtrain, valid, testデータに分割し、validデータでハイパーパラメータチューニング、testデータで精度を算出します。
また、機械学習モデルによってはデータのスケールを合わせる必要があるので、全特徴量を最小値0～最大値1にスケーリングしておきます。

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler

#train_val, testデータに分割
x_train_val_df, x_test_df, y_train_val_s, y_test_s = train_test_split(
    df, y, test_size=0.2, random_state=0, stratify=y
)

#train_valデータからtrain,validデータを作成
x_train_df, x_val_df, y_train_s, y_val_s = train_test_split(
    x_train_val_df, y_train_val_s, test_size=0.1, random_state=1, stratify=y_train_val_s
)

#正規化
scaler = MinMaxScaler()
scaler.fit(x_train_df)
x_train_scaled = scaler.transform(x_train_df)

モデル作成・評価

モデルにはkaggleでおなじみのLightGBMを採用します。
また、Preferred Networks社によってOptunaの拡張機能として開発されたLightGBMのハイパーパラメータ自動最適化モジュール（LightGBM Tuner）を使ってハイパーパラメータチューニングを実施しました。

import optuna.integration.lightgbm as lgb

dtrain = lgb.Dataset(x_train_scaled, label = y_train_s)
dval  = lgb.Dataset(scaler.transform(x_val_df), label = y_val_s)
param = {
        "objective": "multiclass",
        "num_class": 3,
        "metric": "multi_logloss",
        'verbosity': 1,
        'boosting_type': 'gbdt',
        'learning_rate': 0.05
    }
booster = lgb.train(param, dtrain, valid_sets = dval, verbose_eval = 10, early_stopping_rounds = 100)

モデルの性能評価のために、accuracyとconfusion matrixを見てみます。

from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix

import seaborn as sns
import matplotlib.pyplot as plt

import numpy as np

preds = booster.predict(scaler.transform(x_test_df))
y_pred_max = np.argmax(preds, axis=1)
accuracy = accuracy_score(y_test_s, y_pred_max)
print(accuracy)

cm = confusion_matrix(y_test_s, y_pred_max)
cm_matrix = pd.DataFrame(data=cm)
sns.heatmap(cm_matrix, annot=True, fmt='d', cmap='YlGnBu')
plt.xlabel("Prediction", fontsize=13)
plt.ylabel("Ground truth", fontsize=13)

accuracyは0.672でした。目標より1%高い精度でしたが、1%しか変わらないのであればわざわざ機械学習を使わなくても、という気もします…
confusion matrixを見ると、すべての試合を赤コーナー(1)の勝利と予測しているわけではなく、一部データに対しては青コーナー(0)と予想していましたが、正答率はあまり良くなかったです。
また、Draw(3)のサンプル数が極端に少ないためか、Drawと判定した試合は一試合もありませんでした。（これは予想通りでした。）

最後に他の機械学習モデルを組み合わせることで、より高い精度で予測できないか試してみます。
ここでは単純なグリッドサーチでハイパーパラメータを簡易的に選定します。

• k近傍法(KNN)

from sklearn.neighbors import KNeighborsClassifier

param_gs_knn ={'est__n_neighbors':[1, 3, 5, 7, 9, 11, 15, 21], 'est__weights':['uniform', 'distance'], 'est__p':[1, 2]}
best_score = 0
best_params = {}
for n_neighbors in param_gs_knn['est__n_neighbors']:
    for weights in param_gs_knn['est__weights']:
        for p in param_gs_knn['est__p']:
            knn = KNeighborsClassifier(n_neighbors = n_neighbors, weights = weights, p = p)
            knn.fit(x_train_scaled, y_train_s)
            y_pred = knn.predict(scaler.transform(x_val_df)) 
            score = accuracy_score(y_val_s, y_pred)
            if score > best_score:
                best_score = score
                best_params = {'n_neighbors': n_neighbors, 'weights': weights, 'p': p}

knn = KNeighborsClassifier(**best_params)
knn.fit(x_train_scaled, y_train_s)
y_pred_2 = knn.predict(scaler.transform(x_test_df)) 
accuracy = accuracy_score(y_test_s, y_pred)
print(accuracy)

• サポートベクターマシーン(SVC)

from sklearn.svm import SVC

best_score = 0
best_parameters = {}
param_list = [0.001, 0.01, 0.1, 1, 10, 100]

for gamma in param_list:
    for C in param_list:
        svm = SVC(gamma = gamma, C = C)
        svm.fit(x_train_scaled, y_train_s)
        y_pred = svm.predict(scaler.transform(x_val_df)) 
        score = accuracy_score(y_val_s, y_pred)
        if score > best_score:
            best_score = score
            best_parameters = {'gamma' : gamma, 'C' : C}

svm = SVC(**best_parameters)
svm.fit(x_train_scaled, y_train_s)
y_pred_3 = svm.predict(scaler.transform(x_test_df)) 
accuracy = accuracy_score(y_test_s, y_pred_3)
print(accuracy)

最後にLightGBM, KNN, SVCの結果をアンサンブル（多数決）してみます。

tmp = np.array([y_pred, y_pred_2, y_pred_3])
ans = [*map(lambda x:np.argmax(np.bincount(x)), tmp.T)]
accuracy = accuracy_score(y_test_s, ans)
print(accuracy)

最終的な結果は以下の通りで、他のモデルとの組み合わせによる精度向上は見られませんでした。
総合格闘技の技術は飛躍的に進化しており、「強いファイトスタイル」が時代によって異なるので、過去のデータはあまり参考にならないのかも…？

	LightGBM	KNN	SVC	アンサンブル
accuracy	0.672	0.648	0.663	0.672

おわりに

今回は総合格闘技の勝敗予想をする機械学習モデルを作ってみました。判定精度はイマイチでしたが、なんとか目標は達成？できてよかったです。
今後は、少数クラスのオーバーサンプリングやドメイン知識に基づく新たな特徴量生成などを試してみたいです。
とはいえ、格闘技は予想が外れる(アンダードッグがジャイアントキリングする)試合もとても魅力的ですよね。
それでは格闘技ファンの皆さん年末のRIZINを楽しみましょう！ 最後まで読んでいただきありがとうございました！

参考文献

• UFC-Predictions
• Optuna の拡張機能 LightGBM Tuner によるハイパーパラメータ自動最適化
• [Python] k近傍法 (4) グリッドサーチ
• scikit-learn を用いた交差検証（Cross-validation）とハイパーパラメータのチューニング（grid search）